기술기고문
전류 모드 벅 컨버터에 2차 LC 필터를 적용할 때의 모델링 및 제어 방법
전류 모드 벅 컨버터에 2차 LC 필터를 적용할 때의 모델링 및 제어 방법
글: 리키 양(Ricky Yang) / 아나로그디바이스(Analog Devices)
머리말
ADC, PLL, RF 트랜시버를 사용하는 첨단 신호 처리 시스템 설계는 낮은 전력 소모와 높은 시스템 성능을 요구한다. 잡음에 민감한 이러한 디바이스들에 적합한 전원장치를 선택하기란 시스템 설계자에게 항상 어려운 과제이다. 효율과 성능은 어느 한 쪽을 위해 다른 한 쪽이 희생해야 하는 관계이기 때문이다.잡음에 민감한 이들 디바이스를 구동하기 위해서는 전통적으로 LDO 레귤레이터가 사용돼 왔다. LDO 레귤레이터는 시스템 전원공급장치에 종종 존재하는 저주파 잡음을 제거하고 ADC, PLL, RF 트랜시버 같은 디바이스에 깨끗한 전원을 제공할 수 있기 때문이다. 그런데 LDO 레귤레이터는 대개가 효율이 낮다. 특히, LDO 레귤레이터 출력 전압보다 수 볼트 높은 전원 레일로부터 전압을 강하해야 하는 시스템에서는 더욱 그렇다. 이러한 경우, LDO 레귤레이터는 통상적으로 30 ~ 50%의 효율을 나타내는데, 스위칭 레귤레이터를 사용하면 90% 혹은 그보다 더 높은 효율을 달성할 수 있다.
스위칭 레귤레이터는 LDO 레귤레이터보다 효율이 우수지만, 잡음이 심해서 성능을 상당히 희생하지 않고서는 ADC나 PLL을 직접 구동하기가 어렵다. 스위칭 레귤레이터의 잡음 요인 중의 하나가 출력 리플이다. 이것은 ADC 출력 스펙트럼에서 톤(tone)이나 스퍼(spur)로 확연히 나타난다. 따라서 SNR(signal-to-noise ratio)이나 SFDR(spurious-free dynamic range)을 떨어트리지 않으려면 스위칭 레귤레이터의 출력 리플과 출력 잡음을 최소화하는 것이 매우 중요하다.
높은 효율을 유지하면서 동시에 높은 시스템 성능을 달성하기 위해서는 스위칭 레귤레이터 출력에 2차 LC 필터(L2와 C2)를 추가해서 리플과 잡음을 낮추는 것이 바람직하다(그림 1). 하지만 이러한 2스테이지 LC 출력 필터 역시 단점을 가지고 있다. 이 전원 스테이지 전달 함수는 이상적으로 4차수(fourth-order)로 모델링되며, 쉽게 불안정해질 수 있다. 전류 루프의 샘플 데이터 효과를 반영하면, 전체적인 제어-출력(control-to-output) 전달 함수는 5차수인 것으로 나타난다. 이에 대한 솔루션은 1차 LC 필터(L1과 C1)로부터 출력 전압을 검출해서 시스템을 안정화하는 것이다. 하지만 이 방법은 부하 전류가 클 때 2차 LC 필터에 커다란 전압 강하가 가해지기 때문에 출력 전압 레귤레이션이 좋지 않다. 그러므로 애플리케이션에 따라 이 방법이 적합하지 않을 수 있다.
이 글에서는 새로운 하이브리드 피드백 기법을 소개한다. 이 기법은 ADC, PLL, RF 트랜시버에 고효율 고성능 전원을 제공하기 위해 스위칭 레귤레이터에 2차 LC 필터를 사용하는 애플리케이션에서 충분한 안정성 마진을 제공하며, 모든 부하 조건에 대해 출력 정확도를 유지한다.
DC-DC 컨버터에 2차 LC 출력 필터를 사용하는 것에 관한 몇몇 연구 논문들이 나와 있다. 특히 “저전압/고전류 출력을 사용하는 2스테이지 DC-DC 컨버터를 위한 제어 루프 설계”와 “2스테이지 LC 출력 필터를 사용하는 고대역폭 AC 전원을 위한 다중루프 제어 기법에 대한 비교 평가”에서는 2스테이지 전압 모드 컨버터의 모델링과 제어에 관해서 논하고 있다. 이들 연구는 전류 모드 컨버터에는 곧바로 적용될 수 없다. 전류 모드 컨버터에 2차 LC 필터를 적용하는 것에 관해서는 “전류 모드 제어 방식의 컨버터를 위한 2차 LC 필터 분석 및 설계 기법”과 “다중모듈 컨버터 시스템의 3루프 제어”에서 다루고 있다. 다만 이들 논문에서는 2차 인덕터가 1차 인덕터보다 인덕턴스 값이 훨씬 작은 것으로 가정하고 있는데, 실제 애플리케이션에서 항상 그러한 것은 아니다.
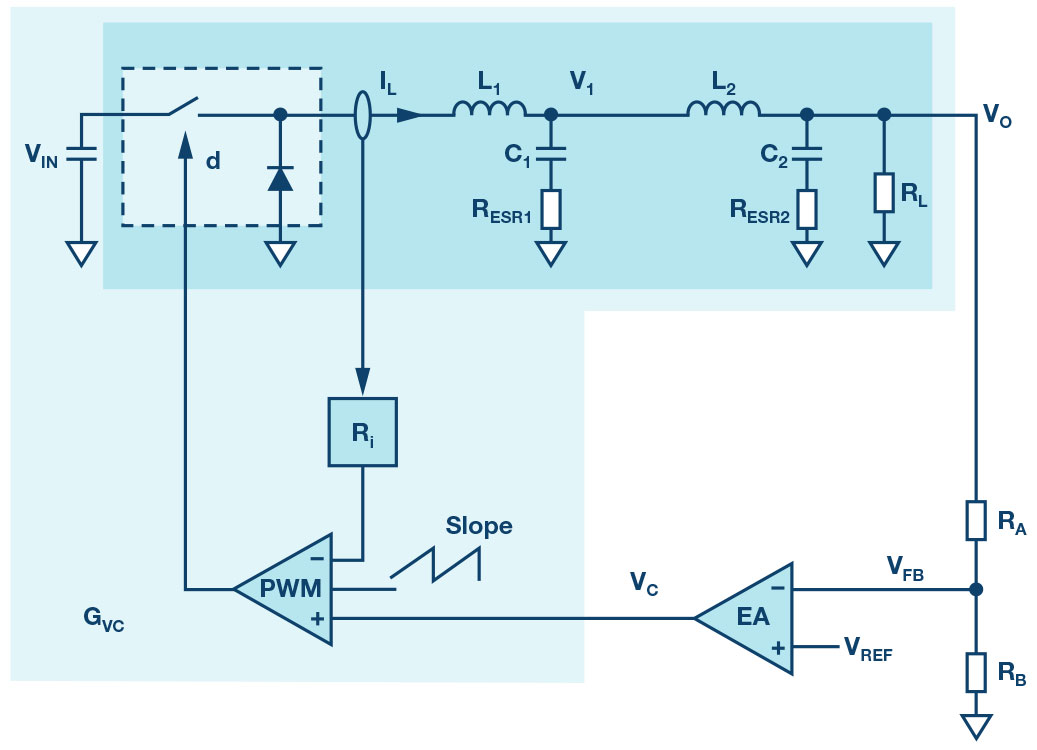
그림 1: 전류 모드 벅 컨버터에 2차 LC 필터를 사용하는 회로도
이 글은 다음과 같이 구성된다:
우선, 벅 컨버터에 2차 LC 필터를 사용할 때의 소신호 모델링을 분석한다. 새로운 5차수 제어-출력 전달 함수를 소개하는데, 이 전달 함수는 주변 인덕터와 커패시터 파라미터에 상관없이 매우 정확하다.
그 다음에는 충분한 안정성 마진을 제공하면서 출력 전압의 우수한 DC 정확도를 유지하는 새로운 하이브리드 피드백 기법을 소개한다. 피드백 파라미터의 한계를 처음으로 분석했는데, 이 분석은 실제 시스템 설계 시 기본적인 판단 기준을 제공할 것이다.
또한 전원 스테이지 소신호 모델과 새로운 하이브리드 피드백 기법을 사용해서 보상 네트워크를 설계하는 방법을 설명한다. 나이퀴스트 플롯을 사용해서 폐루프 전달 함수의 안정성을 평가한다.
전력관리 제품인 ADP5014를 기반으로 간단한 설계 사례를 소개한다. 2차 LC 필터를 사용함으로써 고주파수 대역에서 ADP5014의 출력 잡음이 LDO 레귤레이터보다도 우수하다는 것을 설명한다.
전원 스테이지 소신호 모델링
그림 2는 그림 1의 소신호 블록 다이어그램이다. 제어 루프는 내곽 전류 루프와 외곽 전압 루프로 이루어진다. 전류 루프에서 샘플 데이터 계수 He(s)는 “전류 모드 제어를 위한 새로운 연속 시간 모델”에서 Raymond B. Ridley가 소개한 모델을 참조했다. 그림 2의 간소화한 소신호 블록 다이어그램에서는 입력 전압 외란(voltage disturbance)과 부하 전류 외란(current disturbance)이 0인 것으로 간주한다. 이 글에서는 입력 전압 및 부하 전류와 관련한 전달 함수는 다루지 않기 때문이다.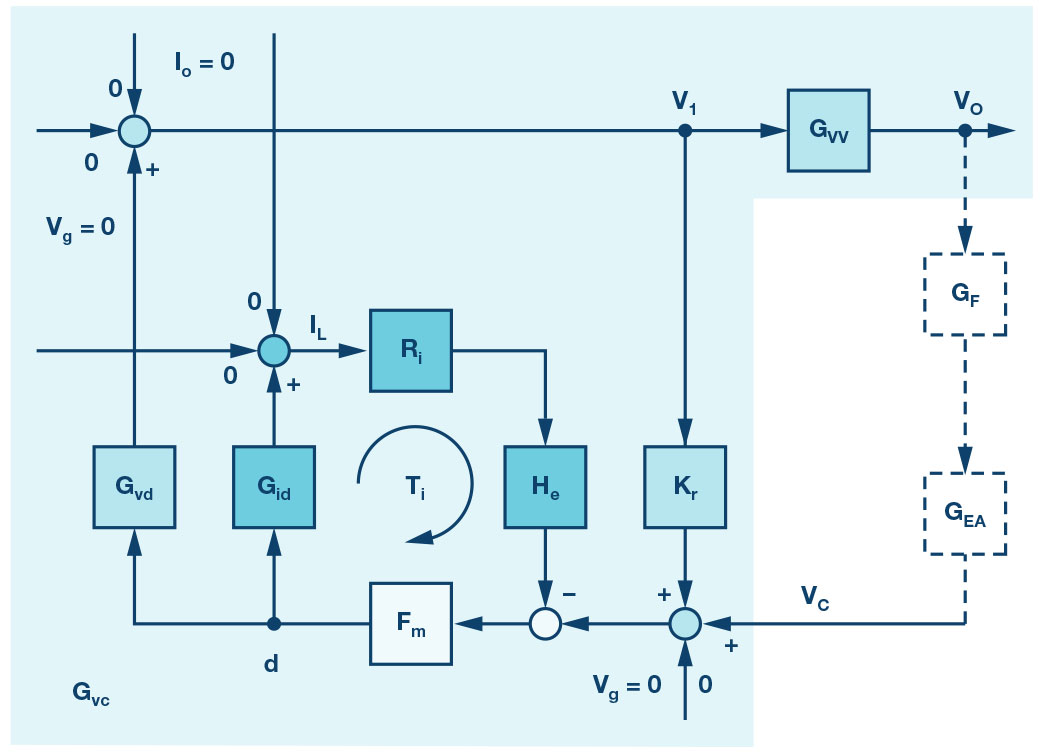
그림 2: 전류 모드 벅 컨버터에 2차 LC 필터를 사용할 때의 소신호 블록 다이어그램
벅 컨버터 사례
이 새로운 소신호 모델을 가지고 전류 모드 벅 컨버터에 다음과 같은 파라미터를 적용했을 때를 살펴보자.? Vg = 5V
? Vo = 2V
? L1 = 0.8μH
? L2 = 0.22μH
? C1 = 47μF
? C2 = 3× 47μF
? RESR1 = 2mΩ
? RESR2 = 2mΩ
? RL = 1Ω
? Ri = 0.1Ω
? Ts = 0.833μs
전류 루프 이득
가장 먼저 살펴볼 전달 함수는 듀티 사이클 변조기 출력에서 측정되는 전류 루프 이득이다. 결과적인 전류 루프 전달 함수는 2쌍의 복소수 켤레 극점을 갖는 4차수 시스템으로 나타나며, 결과적으로 두 개의 시스템 공진점(ω1과 ω2)을 갖는다. 이 두 공진 주파수는 L1, L2, C1, C2에 의해서 결정된다. 도메인 영점은 부하 저항 RL, C1, C2에 의해서 결정된다. 한 쌍의 복소수 켤레 영점(ω3)은 L2, C1, C2에 의해서 결정된다. 또한 전류 루프의 샘플 데이터 계수 He(s)는 스위칭 주파수의 우측 절반(RHP, right half plane) 에서 영점 복소수 쌍을 생성한다.2차 LC 필터를 사용하지 않는 전통적인 전류 모드 벅 컨버터와 비교할 때, 새로운 전류 루프 이득은 한 쌍의 복소수 켤레 극점과 한 쌍의 복소수 켤레 영점을 더 갖는데, 이들 지점은 서로 매우 가깝다.
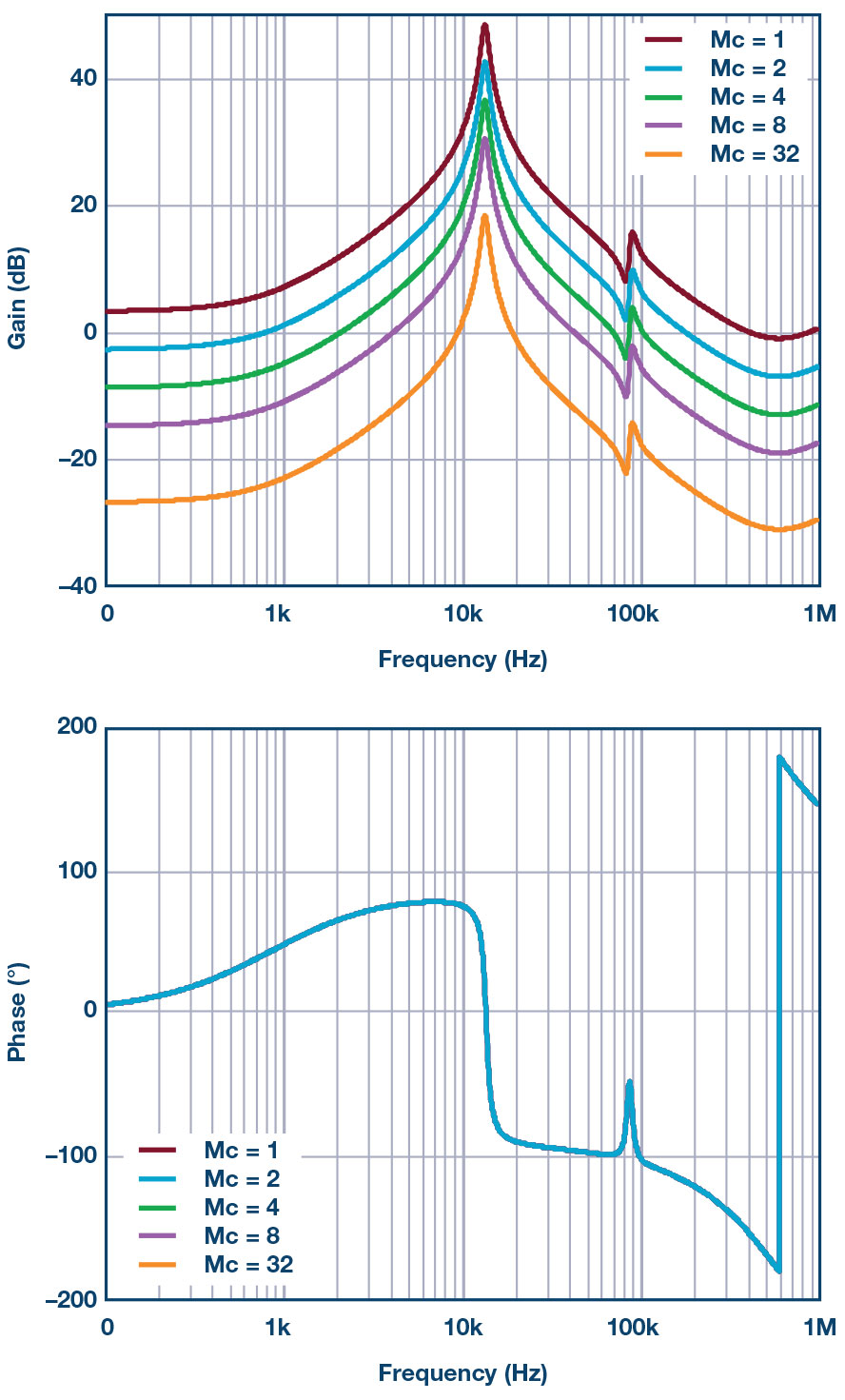
그림 3: 벅 컨버터 전류 루프 이득
그림 3은 각기 다른 외부 램프 값을 갖는 전류 루프 이득을 보여준다. 외부 기울기 보상을 하지 않는 경우에는(Mc = 1) 전류 루프에서 위상 마진이 매우 작다는 것을 알 수 있는데, 이는 부고조파 발진으로 이어질 수 있다. 외부 기울기 보상을 추가하면 이득과 위상 곡선의 형태는 변하지 않으면서 이득의 크기가 감소하고 위상 마진이 증가한다는 것을 알 수 있다.
제어-출력 이득
전류 루프가 닫혔을 때 만들어지는 새로운 제어-출력 전달 함수를 보자. 결과적인 제어-출력 전달 함수는 하나의 도메인 극점(ωp)과 2쌍의 복소수 극점(ωl과 ωh)을 갖는 5차수 시스템으로 나타난다. 도메인 극점은 주로 부하 저항 RL, C1, C2에 의해서 결정된다. 저주파수 켤레 극점 쌍은 L2, C1, C2에 의해서 결정되고, 고주파수 켤레 극점 쌍은 스위칭 주파수의 절반 지점에 위치한다. 또한 각각 C1의 ESR과 C2의 ESR에 의해서 2개의 영점이 생긴다.그림 4는 서로 다른 외부 램프 값을 갖는 제어-출력 루프 이득을 보여준다. 전통적인 전류 모드 벅 컨버터와 비교할 때, 전류 모드 벅 컨버터에 2차 LC 필터를 사용하면 제어-출력 이득에서 한 쌍의 복소수 켤레 극점 쌍(ωl)을 더 갖는다. 추가적인 공진 극점은 최대 180°의 추가적인 위상 지연을 일으킨다. 그러면 위상 마진이 크게 떨어지고, 타입 III 보상을 사용한다고 하더라도 시스템이 불안정해질 수 있다. 이와 함께 그림 4에서는 기울기 보상이 증가할수록 전류 모드에서 전압 모드 제어로 전이한다는 것을 알 수 있다.
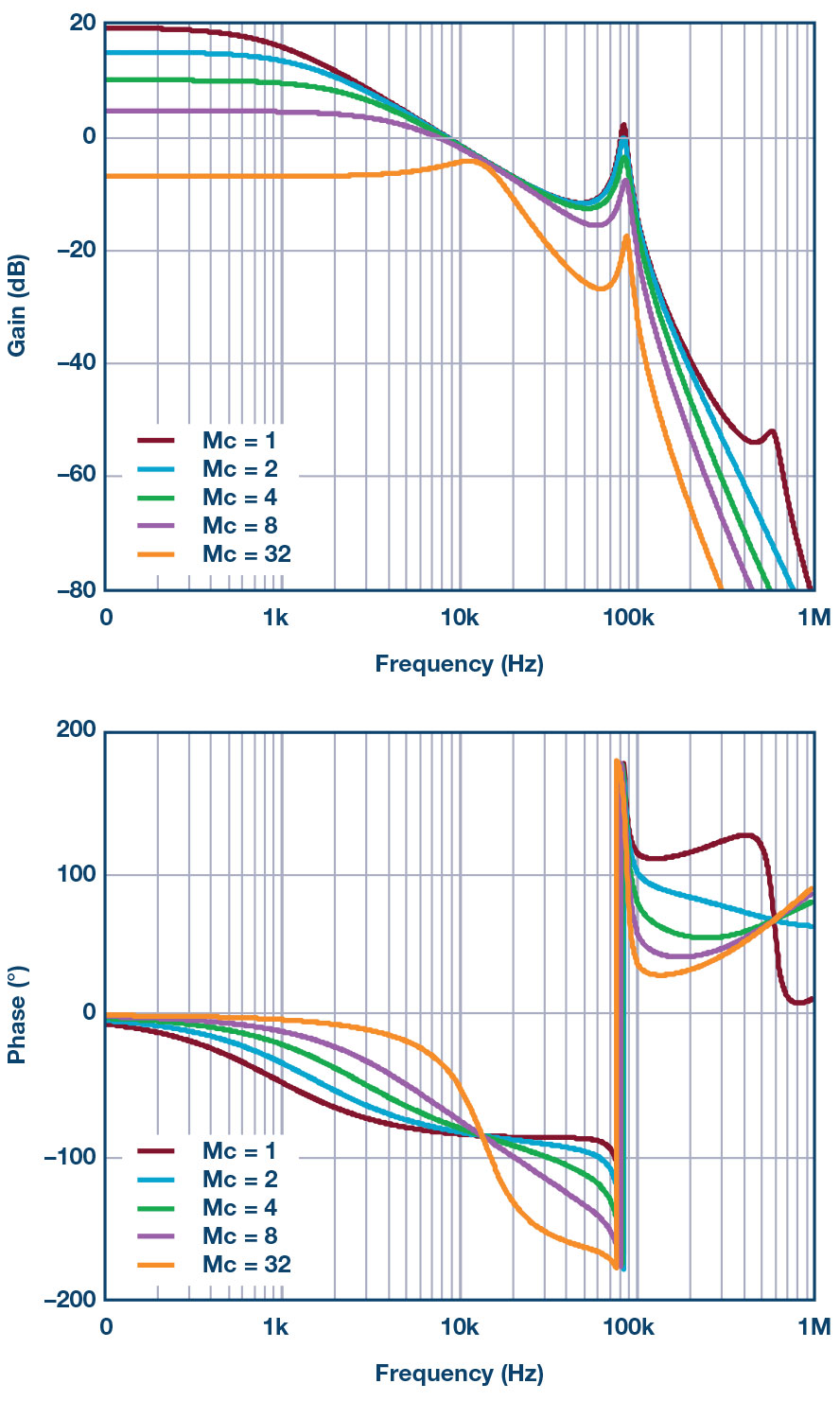
그림 4: 벅 컨버터의 제어-출력 전달 함수
하이브리드 피드백 기법
이번에는 그림 5(a)와 같은 새로운 하이브리드 피드백 구조를 소개한다. 하이브리드 피드백 기법은 1차 LC 필터로부터 추가적인 커패시터 피드백을 사용해서 제어 루프를 안정화하는 것이다. 출력으로부터 저항 분할기를 거친 외곽 전압 피드백은 원격 전압 피드백이라고 하고, 커패시터 CF를 거친 내곽 전압 피드백은 로컬 전압 피드백이라고 한다. 원격 피드백과 로컬 피드백은 주파수 도메인 상에서 서로 다른 정보를 전달한다. 좀더 구체적으로, 원격 피드백은 저주파 신호를 검출해서 출력에 우수한 DC 레귤레이션을 제공하기 위한 것이고, 로컬 피드백은 고주파 신호를 검출해서 시스템에 우수한 AC 안정성을 제공하기 위한 것이다. 그림 5(b)는 그림 5(a)를 간략화한 소신호 블록 다이어그램이다.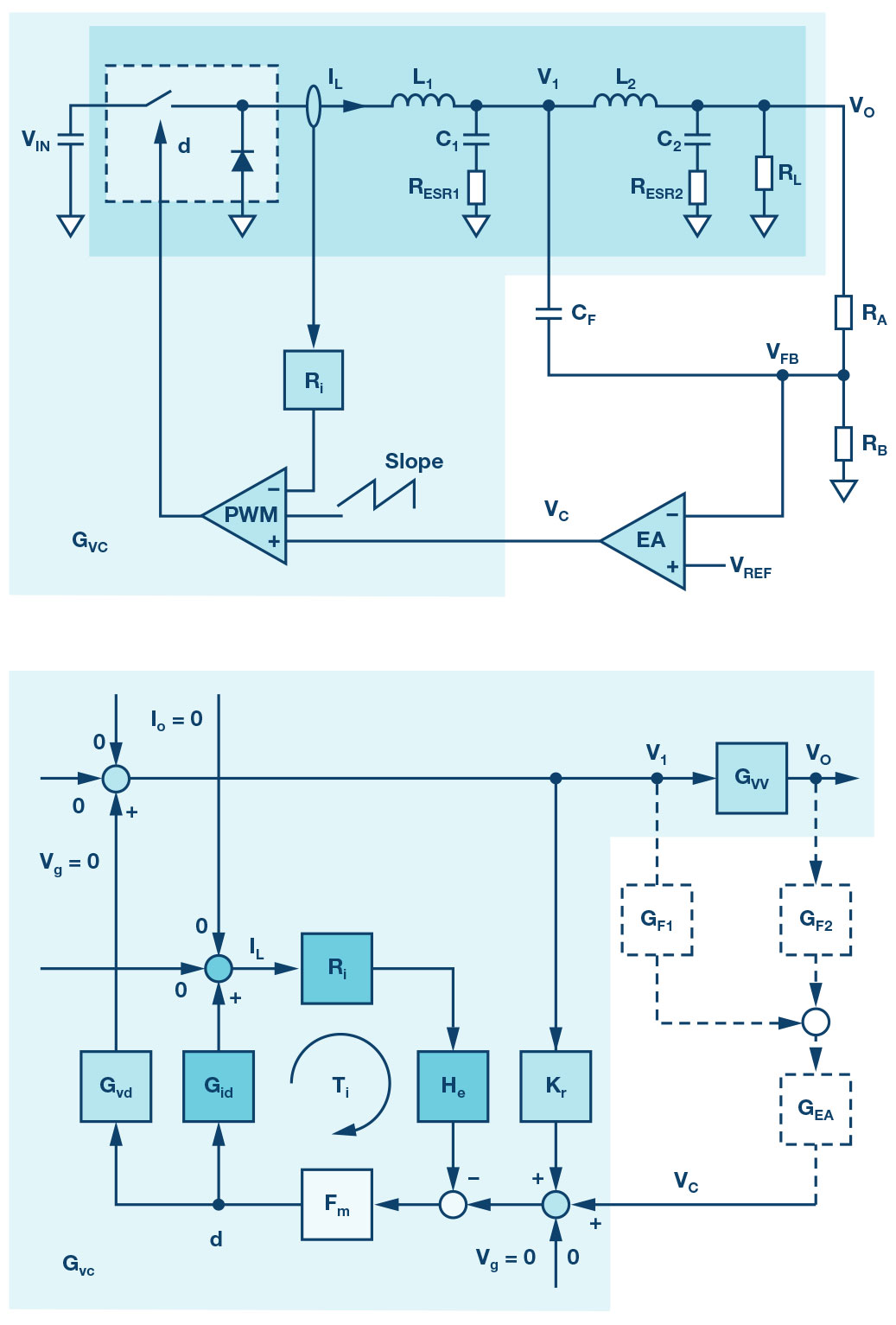
그림 5: 전류 모드 벅 컨버터에 하이브리드 피드백 기법을 적용한 것으로, (a)는 회로 다이어그램이고, (b)는 소신호 모델이다.
피드백 네트워크 전달 함수
하이브리드 피드백 구조의 결과적인 등가 전달 함수는 전통적인 저항 분할기 피드백의 전달 함수하고는 크게 다르다. 새로운 하이브리드 피드백 전달 함수는 극점보다 영점이 더 많고 추가적인 영점들로 인해서 L2와 C2에 의해서 결정되는 공진 주파수 지점에서 180° 위상차를 일으킨다. 따라서 하이브리드 피드백 기법에서는 제어-출력 전달 함수에 있어서의 추가적인 위상 지연이 피드백 전달 함수의 추가적인 영점에 의해서 보상된다. 이는 전체적인 피드백 제어 전달 함수를 기반으로 하는 보상 설계를 손쉽게 설계할 수 있게 해준다.피드백 파라미터의 한계
전원 스테이지의 파라미터들 외에도, 피드백 전달 함수는 2개의 추가적인 파라미터를 포함한다. b는 출력 전압 증폭 비율로서, 이미 널리 알려진 파라미터이다. 이에 반해 α는 전혀 새로운 컨셉트의 파라미터이다.피드백 파라미터 α를 조절함으로써 피드백 전달 함수의 동작을 이해할 수 있다. 그림 6은 α 값이 낮아질 때 피드백 전달 함수에서 영점의 변화 추이를 보여준다. α가 낮아짐에 따라서 한 쌍의 켤레 영점이 LHP(left half plane)에서 RHP(right half plane)로 이동한다는 것을 알 수 있다.
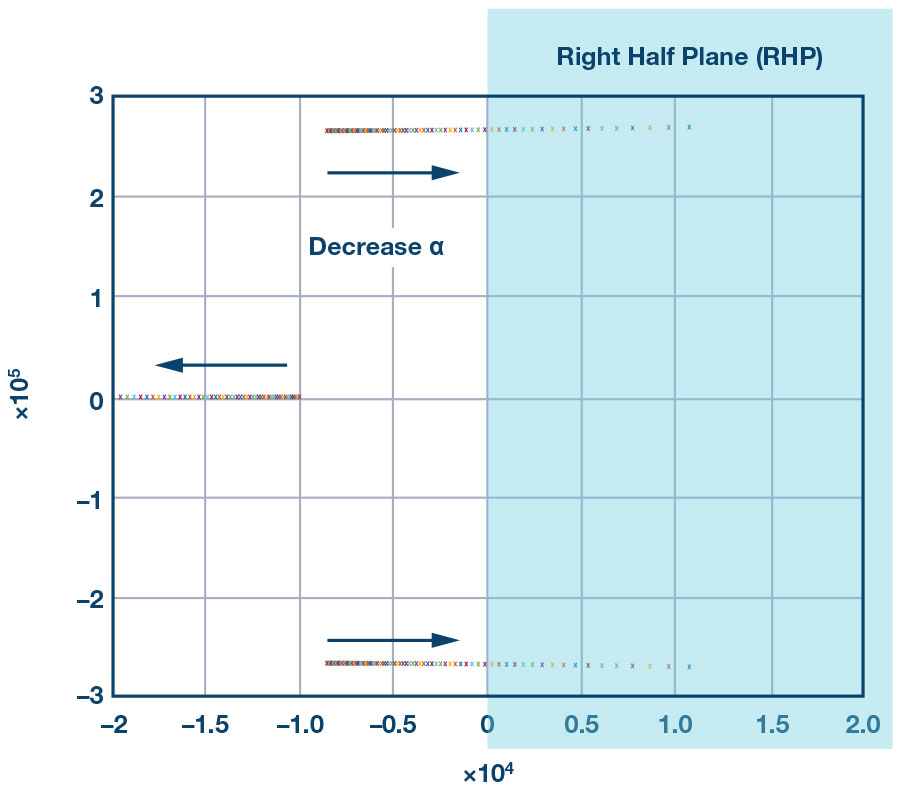
그림 6: 피드백 파라미터 α가 피드백 네트워크 영점에 미치는 영향
그림 7은 서로 다른 α를 갖는 피드백 전달 함수를 보여준다. α를 10-6(예를 들어 RA = 10k, CF = 1nF)으로 낮추면 피드백 네트워크 전달 함수가 180° 위상 지연을 나타내는데, 이것은 복소수 영점이 RHP 영점이 되었다는 것을 의미한다. 이 피드백 전달 함수를 새로운 형태로 좀더 단순화할 수 있다. 영점을 LHP에 유지하려면 파라미터 α는 항상 다음과 같은 조건을 충족해야 한다:
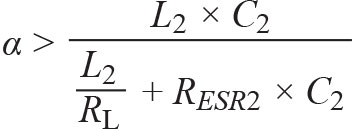(공식 1)공식 1을 사용해서 피드백 파라미터 α의 최소 한계를 계산할 수 있다. 이 조건만 충족한다면 제어 시스템은 안정적일 것이다. 하지만 RA와 CF가 부하 트랜션트 동안 출력 전압 변동에 대한 RC 필터로서 동작하기 때문에 α가 너무 크면 부하 트랜션트 성능을 떨어트릴 것이다. 그러므로 α가 너무 커서는 안된다. 실제 설계에서는 α를 최소 한계 값보다 20 ~ 30% 높게 할 것을 권장한다.
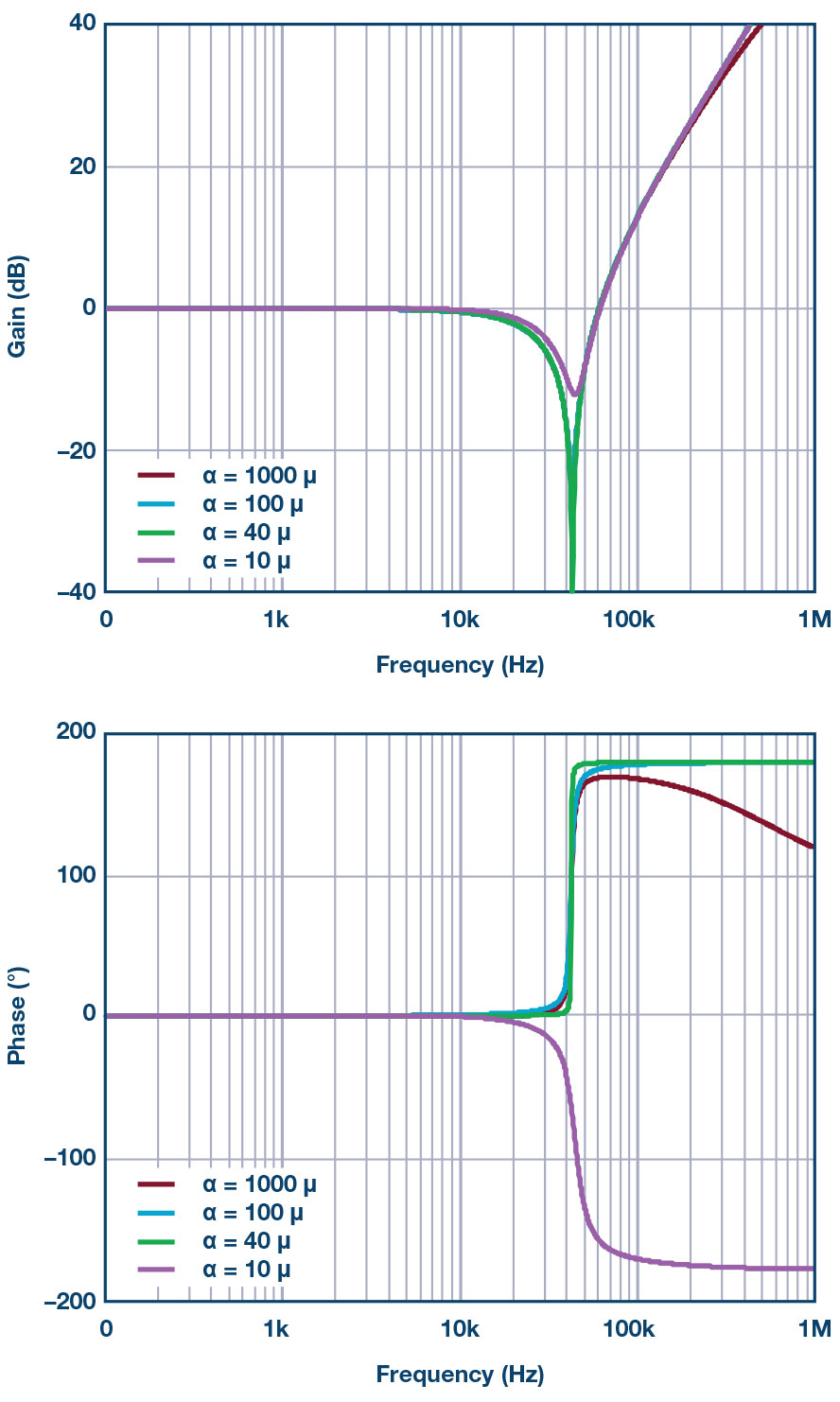
그림 7: 서로 다른 α 값을 갖는 하이브리드 피드백 네트워크의 전달 함수
루프 보상 설계
보상 설계
제어-출력 전달 함수 Gvc(s)와 피드백 전달 함수 GFB(s)를 곱해서 제어-피드백 전달 함수 GP(s)를 도출할 수 있다. 보상 전달 함수 GC(s)는 하나의 영점과 하나의 극점을 갖도록 설계한다. 그림 8은 제어-피드백 및 보상 전달 함수와 폐루프 전달 함수 TV(s)의 점근적 보드 선도(asymptotic Bode plot)을 보여준다. 보상 전달 함수는 다음과 같은 순서로 설계한다.교차 주파수(fc)를 계산한다. 대역폭이 fZ1에 의해서 제한되기 때문에 fZ1보다 낮은 fc를 선택할 것이 권장된다.
fc일 때 GP(s)의 이득을 계산한다. 그런 다음에 GC(s)의 중간 주파수 대역 이득은 GP(s)와 숫자가 반대여야 한다.
보상 영점이 전원 스테이지의 도메인 극점(fP1)에 오도록 한다.
보상 극점이 출력 커패시터 C1의 ESR에 의해서 결정되는 영점(fZ2)에 오도록 한다.
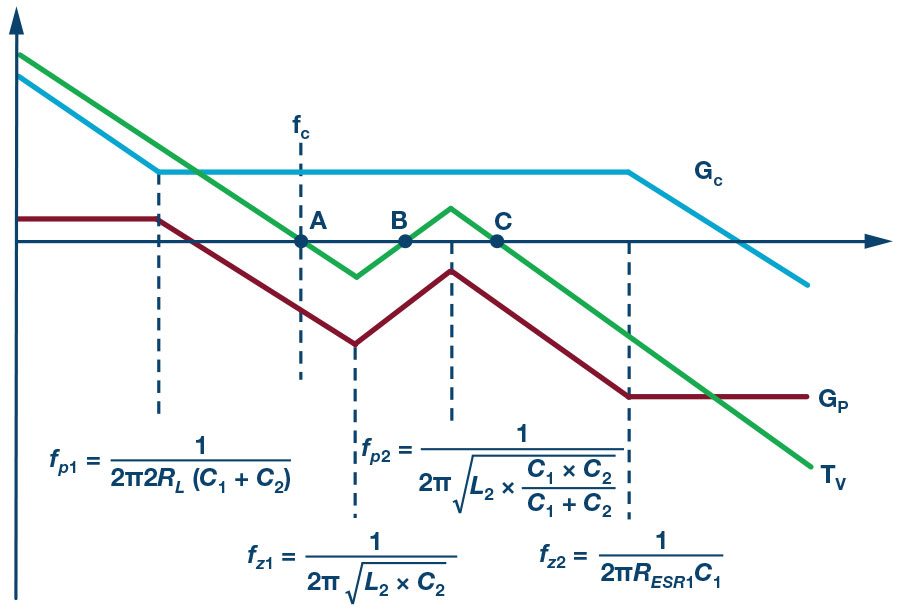
그림 8: 제어-출력 및 하이브리드 피드백 전달 함수에 기반한 루프 이득 설계
나이퀴스트 플롯을 사용한 안정성 분석
그림 8에서는 폐루프 전달 함수 TV(s)가 0dB를 3번 지난다는 것을 알 수 있다. 그림 9에서 보듯이, 나이퀴스트 플롯을 사용해서 폐루프 전달 함수의 안정성을 분석할 수 있다. 이 플롯은 (-1, j0)으로부터 멀리 떨어져 있으므로 폐루프가 안정적이며 위상 마진이 충분하다는 것을 알 수 있다. 나이퀴스트 플롯에서 A, B, C 지점은 보드 선도에서 A, B, C 지점에 해당된다.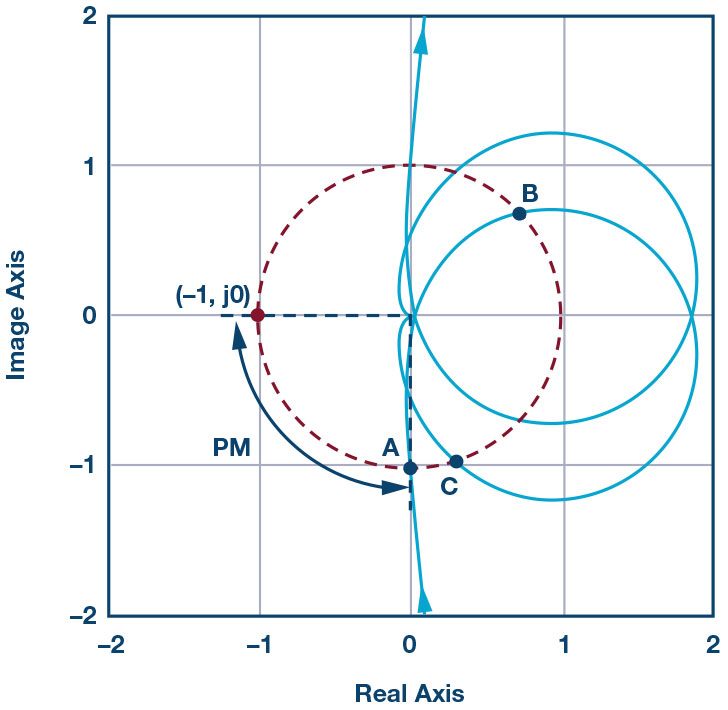
그림 9: 폐루프 전달 함수의 나이퀴스트 플롯
설계 예시
ADP5014는 저주파수 대역에서 출력 잡음을 낮추기 위해 여러 개의 아날로그 블록들을 최적화한다. 또한 단위 이득 전압 레퍼런스 구조이므로, VOUT 설정이 VREF 전압보다 낮은 경우 출력 잡음은 출력 전압 설정과 무관하다. 2차 LC 필터를 추가함으로써 고주파수 대역에서 출력 잡음을 감쇠할 수 있는데, 특히 기본 스위칭 리플과 고조파를 감쇠할 수 있다. 그림 10은 설계 예시를 나타낸 것이다.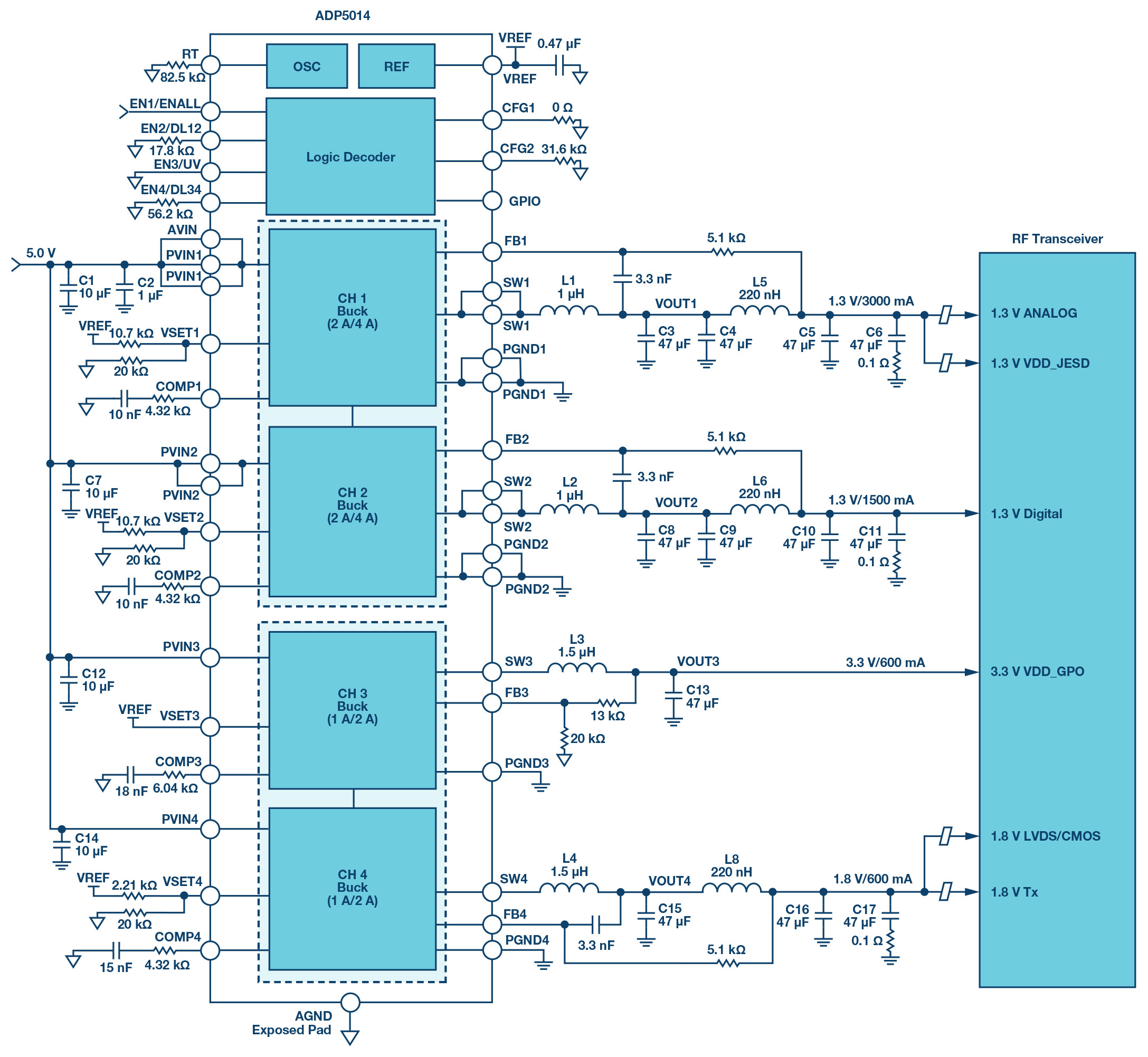
그림 10: ADP5014에 2차 LC 필터를 사용한 RF 트랜시버
그림 11은 10Hz~10MHz 주파수 범위에서 ADP5014의 잡음 스펙트럼 밀도와 10Hz~1MHz 주파수 범위에서 적분 rms 잡음을 측정한 결과를, 또 다른 전통적인 2A 저잡음 LDO 레귤레이터인 ADP1740과 비교해서 나타낸 것이다. 고주파수 대역에서 ADP5014의 출력 잡음이 ADP1740보다도 더 우수하다는 것을 알 수 있다.
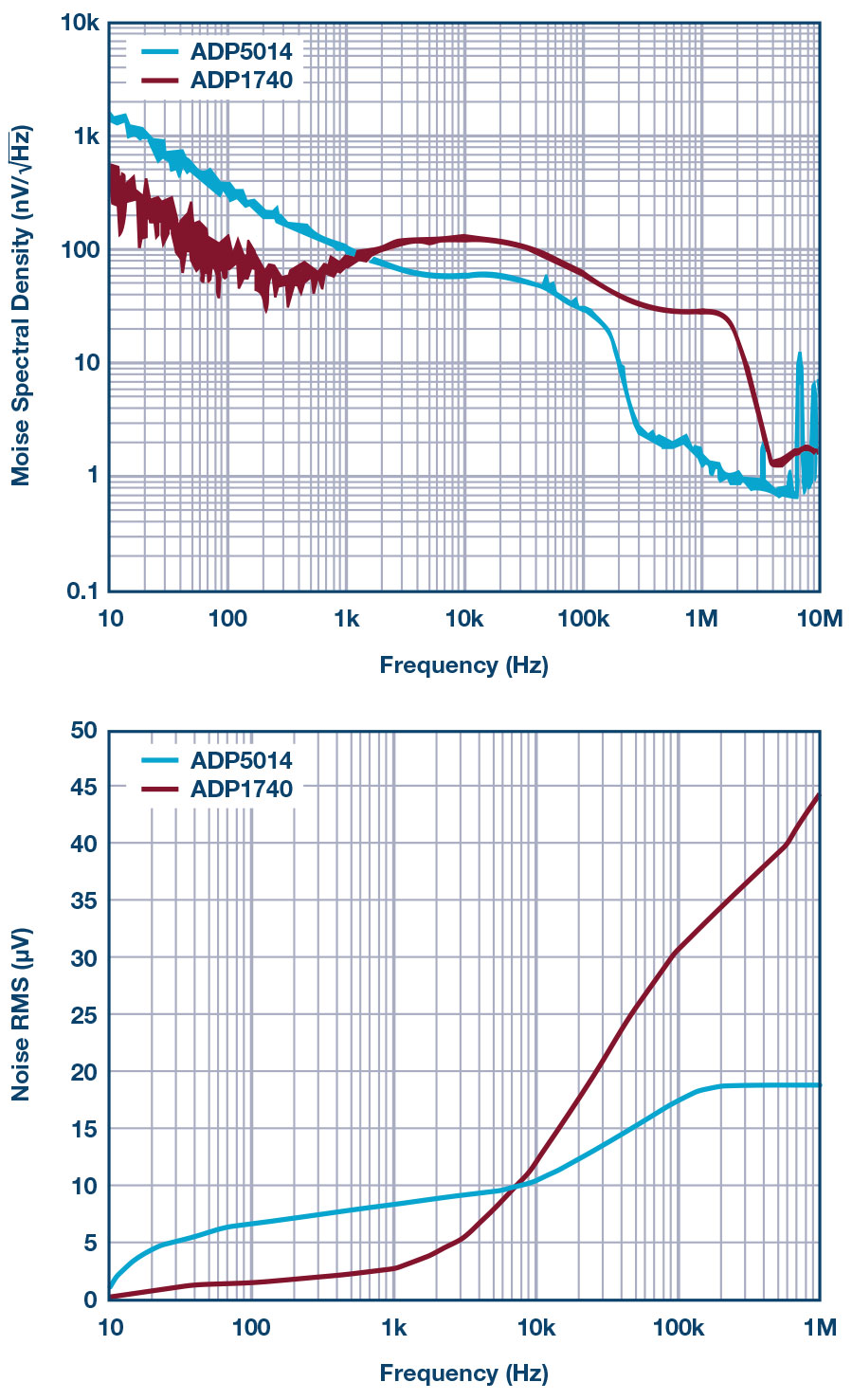
그림 11: ADP5014와 ADP1740의 출력 잡음 성능 비교. (a)는 잡음 스펙트럼 밀도이고, (b)는 적분 rms 잡음이다.
맺음말
이 글에서는 전류 모드 벅 컨버터에 2차 LC 출력 필터를 사용할 때의 모델링과 제어에 대해서 설명하고 제어-출력 전달 함수를 분석해 보았다. 또한 새로운 하이브리드 피드백 구조를 소개하고 피드백 파라미터 한계에 대해서 살펴보았다.스위칭 레귤레이터에 2차 LC 필터와 하이브리드 피드백 기법을 적용함으로써 LDO 레귤레이터에 필적하거나 또는 그보다 더 우수한 성능의 깨끗하고 안정적인 전원을 제공할 수 있다는 것을 확인하였다.
이 글은 주로 전류 모드 벅 컨버터에 대해서 다루고 있으나, 여기에서 설명한 기법들을 전압 모드 벅 컨버터에도 적용할 수 있다.
제품스펙