글: 피터 딜로스(Peter Delos) 테크니컬 리드, 마이크 존스(Mike Jones) 수석 전기 설계 엔지니어 / 아나로그디바이스(Analog Devices, Inc.)

 

개요

이 글에서는 대규모 다채널 시스템에서 위상 잡음을 예측하기 위한 체계적 접근법을 설명하고, 16채널 S-밴드 데모를 통해 측정 결과를 비교한다. 이 분석적 접근법의 뼈대는, 일련의 측정 값을 토대로 해서 상관 잡음과 비상관 잡음을 계산할 수 있다는 것이다. 그럼으로써 다양한 조건 하에서 위상 잡음을 예측할 수 있다. 이 글에서는 16채널 데모를 통해 설명한다. 하지만 특정 설계마다 구성이 다를 수 있으므로, 각각의 구성을 고려해서 시스템 잡음을 분석해야 한다. 이 글은 RF 시스템에서 위상 잡음 최적화에 관한 일련의 논문들을 참고했다1-6. 관련 자료들은 참고문헌으로 밝혔다.

 

들어가며

위상 잡음(phase noise)은 모든 RF 시스템 설계에서 중요한 성능 지표이다. 채널들을 코히어런트하게 결합한 위상 배열 같은 대규모 다채널 RF 시스템에서 한 가지 과제가, 분산적인 수신기와 송신기를 코히어런트하게 결합해서 어레이 차원에서 향상된 동적 범위를 달성하도록 하는 것이다. 그러기 위해서는 시스템 엔지니어링 작업할 때 시스템에서 상관 잡음 요소와 비상관 잡음 요소들을 고려해야 한다. 이 글은 대규모 시스템에서 잡음 성능 예측을 위한 분석 기법을 개발하고자 하는 시스템 엔지니어들을 돕기 위한 것으로서, 16채널 RF 데모를 예로 들어서 위상 잡음을 예측하기 위한 체계적인 접근법을 설명한다.

 

위상 배열 내의 모든 신호는 채널들 간에 비상관적 잡음 요소와 상관적 잡음 요소를 모두 포함한다. 분산된 부품들의 부가적인 잡음은 비상관적이다. 하지만 분산된 부품들 간에 공유되는 공통 신호는 상관적 잡음 성분을 발생시킨다. 여기서 과제는 아키텍처에서 상관 잡음 성분들을 어떻게 해야 신속하게 파악할 수 있는가이다. 공통적인 것이든 공유되는 것이든 이것들은 채널들 간에 상관 잡음을 일으킬 것이다. 이러한 것으로서 공유 LO, 클럭, 전원을 들 수 있다. 시스템의 복잡성이 높아질수록 이러한 잡음 성분들을 추적하기가 어려워진다. 따라서 잡음 관점에서 빠르게 아키텍처를 파악하고 상관 잡음을 예측할 수 있는 직관적인 기법이 차세대 시스템을 설계하는 시스템 엔지니어들에게 필요하다.

 

이 글에서는 16채널 S-밴드 시스템으로 이 접근법을 예시하고, 몇 가지 경험적 측정만으로 다양한 채널 결합 조건 하에서 위상 잡음을 훌륭하게 예측할 수 있다는 것을 보여줄 것이다. 이 경험적 모델의 핵심 포인트 중 하나는 몇 가지 측정이 필요하다는 점이다. 부품 시뮬레이션에서 곧바로 대규모 다채널 위상 잡음 예측으로 넘어가 우수한 정확도를 달성한다는 것은 어려운 일이다. 그런데 이 접근법은 단 몇 가지 측정 값을 가지고서 상관 및 비상관 잡음을 도출하고 다채널 위상 잡음을 상당 수준의 정확도로 예측할 수 있다. 16채널 S-밴드 데모의 경우, 측정 결과가 모델 예측과 1dB 이내로 일치하는 것으로 확인된다.

 

상관 잡음과 비상관 잡음

자유 공간에서든 RF 프로세싱에서든, 신호들을 결합하면 각 신호의 잡음이 다음과 같이 합쳐진다:

 

이 공식에서 c는 상관 계수로서 -1에서 +1까지다. c = -1이면 잡음이 상쇄된다. c = 0이면 잡음은 비상관적이고, c = 1이면 잡음은 완벽하게 상관적이다.

 

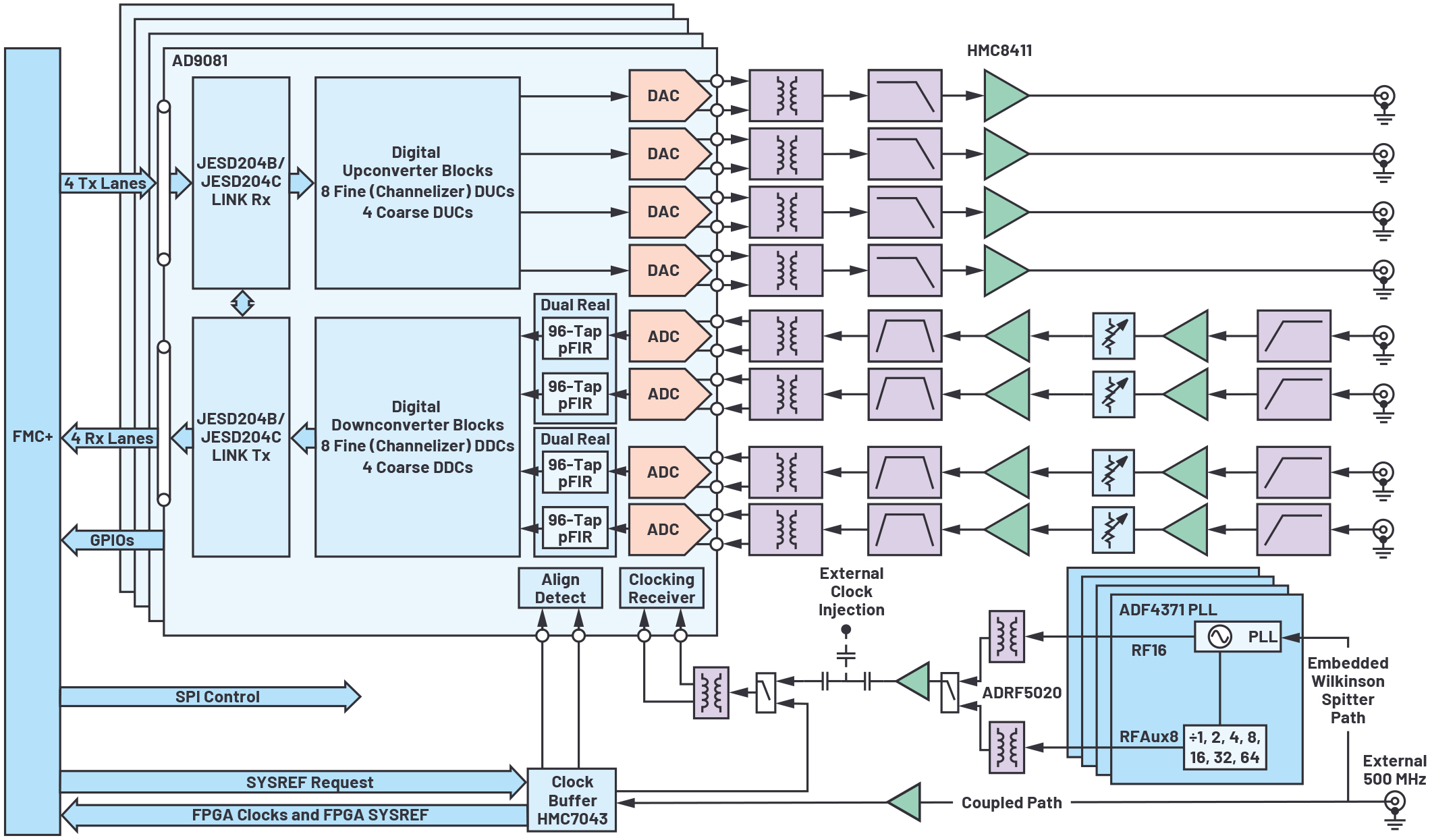
그림 1: 16채널 데모. 이 플랫폼은 4개의 AD9081 IC를 포함한다. 각 AD9081이 각각 4개씩의 RF DAC와 RF ADC를 제공하므로, 총 16개의 송신 및 16개 수신 채널을 제공한다.

 

▶ 잡음 성분이 비상관적이면(c = 0), 이 잡음은 10logN으로 증가한다. 신호 레벨이 20logN의 비율로 증가한다면(잡음보다 10logN 큰 비율) 결과적인 SNR 향상은 10logN이다.

 

▶ 잡음 성분이 상관적이면(c = 1), 잡음은 20logN으로 신호와 같은 비율로 증가하고 어떠한 SNR 향상도 이룰 수 없다. 이것은 분산 시스템용으로는 바람직하지 않다.

 

▶ 잡음 상쇄 회로에서는 음의 상관 계수가 발생한다. 이 경우는 공식(1)을 위해 언급한 것일 뿐, 더 이상의 설명은 생략한다.

 

실제로 대규모 분산형 시스템에서 잡음 성분들은 채널들 간에 부분적으로 상관적이다. 그러므로 시스템 차원의 잡음 모델을 개발하기 위한 효과적이면서도 직관적인 접근법이 필요하다.

 

16채널 데모

다채널 환경에서 최신 고속 데이터 컨버터를 평가하기 위해 16채널 다이렉트 S-밴드 RF 샘플링 플랫폼을 개발했다. 이 플랫폼은 4개 AD9081 MxFE®(mixed-signal front end) IC를 포함한다. 각 AD9081은 4개씩의 RF DAC와 RF ADC를 제공하므로, 총 16개씩의 송신 및 수신 채널을 제공한다.

 

이 16채널 평가 플랫폼은 4개의 MxFE IC를 포함하므로 Quad-MxFE라고 명명했다. 그림 1과 그림 2는 전체적인 블록 다이어그램과 보드 모습을 보여준다.

 

그림 2: 16채널 데모 보드인 Quad-MxFE

 

다채널 위상 잡음 모델

그림 1의 16채널 개발 플랫폼 블록 다이어그램에서는 다양한 기능들을 볼 수 있다. 하지만 이 다이어그램으로는 상관 잡음과 비상관 잡음을 한 눈에 파악하기가 어렵다. 따라서 잡음 관점에서 이 아키텍처를 다시 그릴 필요가 있다. 그럼으로써 모든 채널들 간에 공통적인 잡음 성분, 일부 채널들에 걸쳐서 상관적인 잡음 성분, 채널들에 걸쳐서 비상관적인 잡음 성분을 체계적으로 파악할 수 있다. 그림 3은 16채널 개발 플랫폼의 일러스트로서, 이러한 세 가지 범주의 잡음 요소들을 구분해서 보여준다.

 

▶ 클럭 잡음: 이 Quad-MxFE로는 다양한 클럭 구성이 가능하다. 그러므로 위상 잡음 모델에 그 특정한 구성을 반영시켜야 한다. 이 테스트에서는 모든 채널에 하나의 공통적인 저잡음 클럭을 사용하거나 또는 4개의 MxFE 각각에 개별적인 ADF4371 PLL 합성기를 클럭 입력으로 사용하는 구성을 적용했다. 하나의 공통 클럭을 사용하는 경우에는, 이 잡음이 모든 16개 결합 채널들에 상관적일 것이다. 이와 달리, 각 MxFE마다 개별적으로 4개의 ADF4371 PLL을 사용하는 경우에는, PLL 잡음이 각 MxFE 차원에서는 상관적이지만 여러 MxFE들에 걸쳐서는 상관적이지 않고, 반면에 레퍼런스 잡음은 모든 채널들에 걸쳐서 상관적일 것이다.

 

■ 피터 딜로스(Peter Delos)의 글 “분산형 PLL을 사용하는 위상 배열을 위한 시스템 레벨 LO 위상 잡음 모델”에서는 분산형 PLL을 사용할 때의 분석 기법에 대해서 설명하고 있다. 이 글에서는 레퍼런스 주파수, 분배 시스템, PLL 회로의 잡음 성분과 PLL 루프 대역폭의 영향에 대해서 다루고 있다.

 

▶ 각 MxFE 차원의 상관 잡음: 이 잡음은 MxFE 내의 각 채널에 대해 상관적인 MxFE의 잡음이다. 각 MxFE의 상관 잡음은 IC 내에서 공통적인 부가 잡음과 IC 내의 채널들에 걸쳐서 공통적인 전원의 영향을 포함한다.

 

▶ 각 채널의 비상관 잡음: 이 잡음은 각 채널 차원의 서로 다른 잡음이다. 이 잡음은 DAC 코어와 모든 증폭기 잔존 위상 잡음을 포함한다. 공식 2에서 ‘TXNoise’로 표기하고 있는 부분이다.

 

위에서 열거한 위상 잡음 요소들을 토대로 해서 종합적인 위상 잡음을 다음과 같이 계산할 수 있다:

 

 

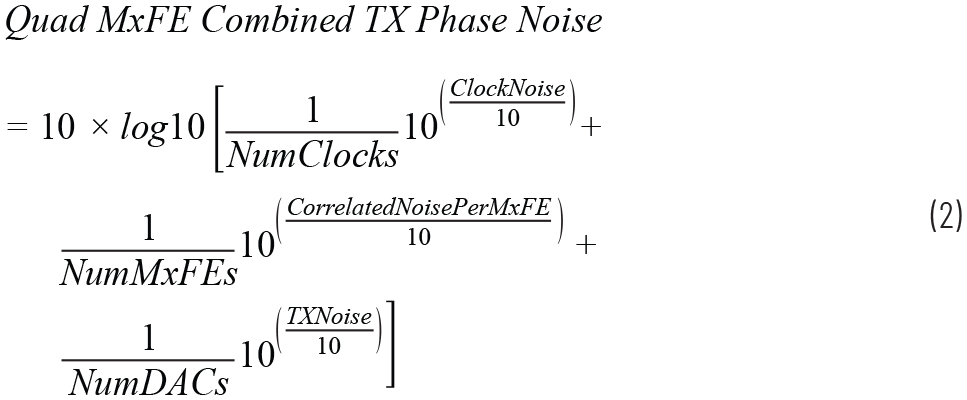
다음은, 이 테스트베드로 모델을 이러한 형태로 단순화하기 위한 몇 가지 부연 설명이다:

 

▶ 전원장치의 영향: 위상 잡음이 낮은 설계에서는 전원장치 위상 잡음이 상당한 잡음 요인이 될 수 있다. “전원장치 변조 비율 파헤쳐보기: PSMR과 PSRR은 어떻게 다른가?”와 “향상된 DAC 위상 잡음 측정으로 위상 잡음이 극히 낮은 DDS 애플리케이션 달성하기”에서는 전원장치 잡음 문제에 대해서 다루고 있다. 이 글의 분석에서는 전원장치의 영향이 미미한 것으로 간주하고 있다. 만약 전원장치 잡음이 IC들에 상당한 위상 잡음을 발생시키는 요인이고 채널들 간에 걸쳐서 공유된다면 각 MxFE 차원의 상관 잡음과 마찬가지로 이 영향을 상관 잡음 요소로서 반영해야 할 것이다. 

 

▶ 레퍼런스 오실레이터 잡음: “분산형 PLL을 사용하는 위상 배열을 위한 시스템 레벨 LO 위상 잡음 모델”에서 언급하고 있듯이, 대규모 시스템에서는 레퍼런스 오실레이터 잡음을 반영해야 한다. 이 테스트베드로는 위상 잡음이 극히 낮은 레퍼런스를 사용했다. 이 잡음은 다른 잡음 요소들에 비해서 훨씬 낮으므로 공식에는 포함시키지 않았다.

 

모델에 사용할 측정 값 구하기

공식 2와 같은 종합적 위상 잡음 모델을 도출한 다음에 할 일은 이 공식으로 사용할 잡음 값을 구하는 것이다. Quad-MxFE 테스트베드의 경우에는 다음과 같은 3가지 측정 값을 사용해서 필요한 정보를 도출할 수 있다:

▶ 클럭 소스의 절대 위상 잡음

▶ MxFE들에 걸친 잔존 위상 잡음

▶ 동일 MxFE 내에서 채널들에 걸친 잔존 위상 잡음

 

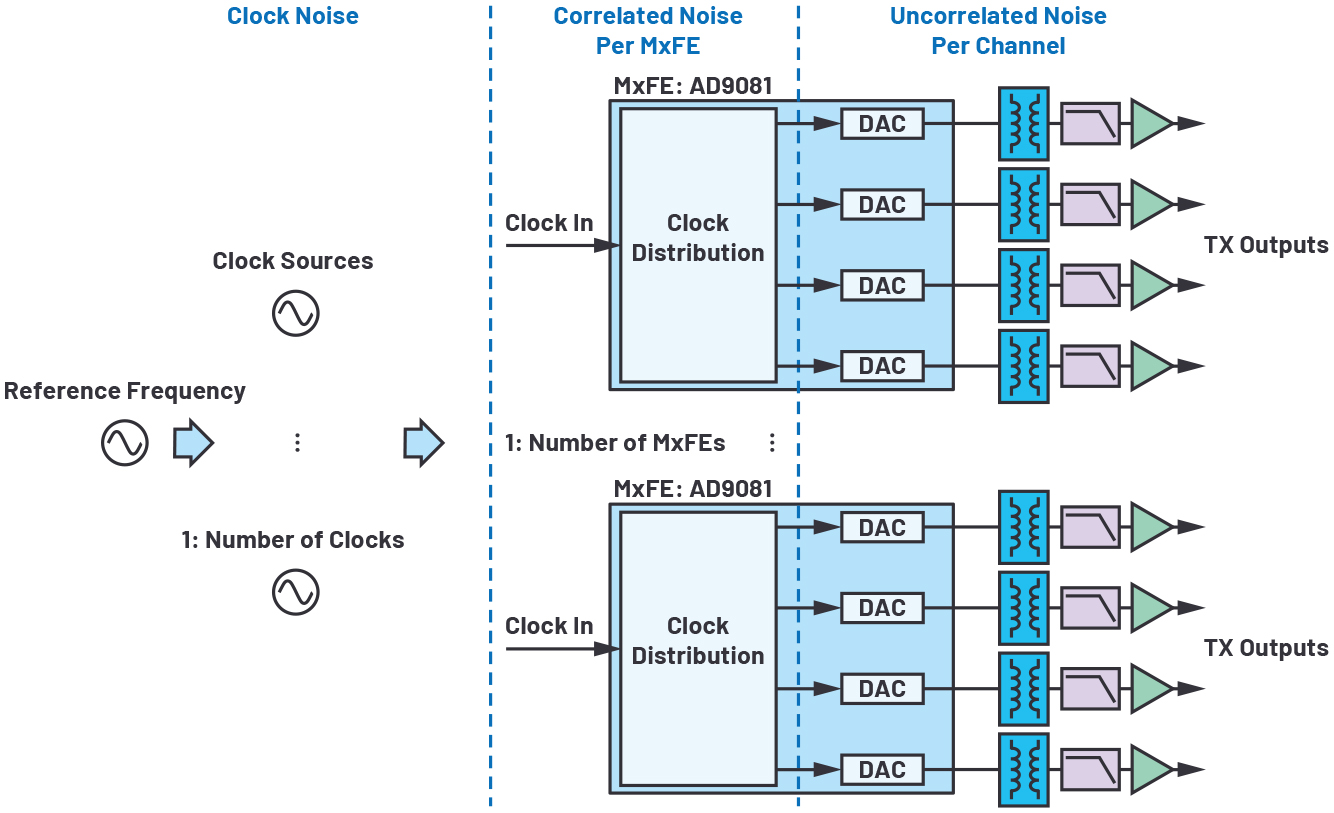
그림 3: 그림 1을 클럭 위상 잡음의 관점에서 다시 그린 다이어그램

 

그림 4는 이 측정 값들을 얻기 위한 테스트 설정을 나타낸 것이다. 그림 4(b)와 그림 4(c)는 공통 클럭 소스가 상쇄된 잔존 잡음 측정을 보여준다. 단일 MxFE 내에서 잔존 위상 잡음을 측정할 때도 그 MxFE 내에서 채널들에 걸친 상관 잡음은 제거되고 측정된다. 하지만 MxFE들에 걸친 잔존 위상 잡음을 측정할 때는 MxFE에서 상관 잡음이 측정으로 포착된다.

 

다음으로 할 일은 이렇게 측정된 데이터를 가지고 공식 2에서 필요로 하는 세 가지 잡음 요소를 계산하는 것이다:

1. 클럭 잡음 = 클럭 위상 잡음 측정(그림 4(a)) + 20log(FOUT/FCLOCK)

2. 각 MxFE 차원의 상관 잡음 = MxFE들에 걸친 잔존 위상 잡음(그림 4(b)) - 동일 MxFE 내의 잔존 위상 잡음(그림 4(c)). 이 계산을 위해서는 선형 전원으로 환산하고 뺀 다음, 다시 dB로 환산해야 한다. 그러므로 10log(10^(MxFE들에 걸친 잔존 위상 잡음/10) - 10^(동일 MxFE 내의 잔존 위상 잡음/10))이다.

3. TxNoise = 동일 MxFE 내의 잔존 위상 잡음(그림 4(c))

 

잔존 위상 잡음 측정에 관한 부연 설명: 이 하드웨어를 가지고, 우리는 2번 항목과 3번 항목의 잡음 성분은 주파수에 따라서 증감한다 것을 알게 됐다. 그러므로 다른 주파수로 전환할 때는 추가적인 20log(FOUT/FMEAS)가 필요하다. 이것은 모든 하드웨어가 그러한 것은 아니고 설계마다 다를 수 있다.

 

측정 사례 1: 공통적으로 낮은 위상 잡음 클럭 사용

이 측정은 전체적인 16채널 데모에 하나의 공통적인 저잡음 12GHz 클럭을 사용했다. 클럭 소스는 SMA100B로서, 그림 1에서 외부 클럭 주입 노드로 연결했다. 표시한 조건들은 3.2GHz 송신 출력 주파수를 사용할 때이다. 

 

그림 5(b)를 보면, MxFE들에 걸친 상관 잡음이 가장 큰 비중을 차지한다는 것을 알 수 있다. 이 시스템에 MxFE를 추가하면 이 잡음이 향상되다가, 공통 클럭 잡음에 의해 제한될 것이다. 각 잡음 요소의 곡선 형태를 보면 곡선을 따라서 몇몇 지점들만 추가하는 것은 정확한 예측을 달성하는데 충분치 않은 것으로 생각되어서 공식 2에 그림 5(b)의 데이터를 곧바로 사용하는 것이 좋겠다고 생각했다. 그런 다음에는 이 모델을 검증하기 위한 측정을 실시했다. 그 결과, 이 모델의 예측이 놀랄 만큼 정확하다는 것을 확인할 수 있었다. 그림 6  ~ 8은 이 측정 결과를 보여준다.

 

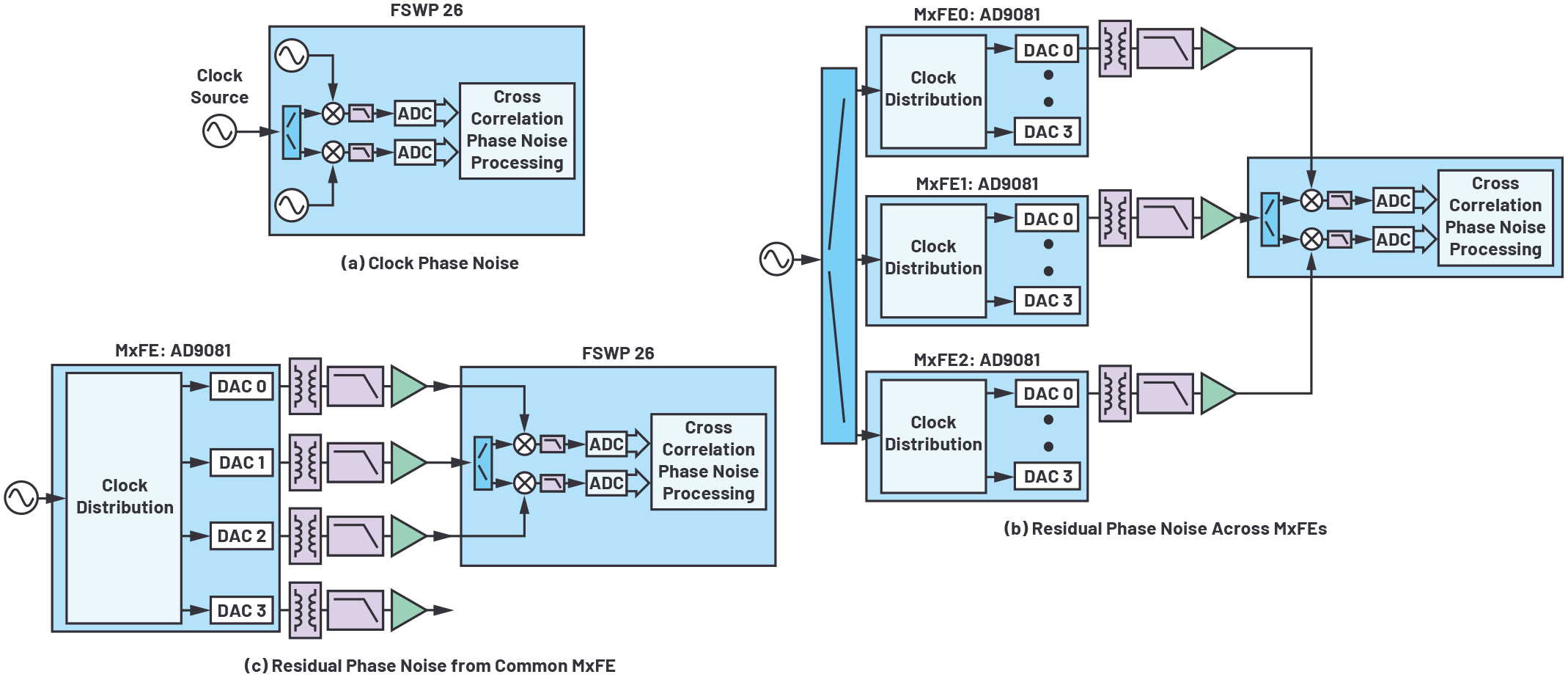
그림 4: 이 위상 잡음 모델에는 세 가지 측정 값들이 사용됐다.

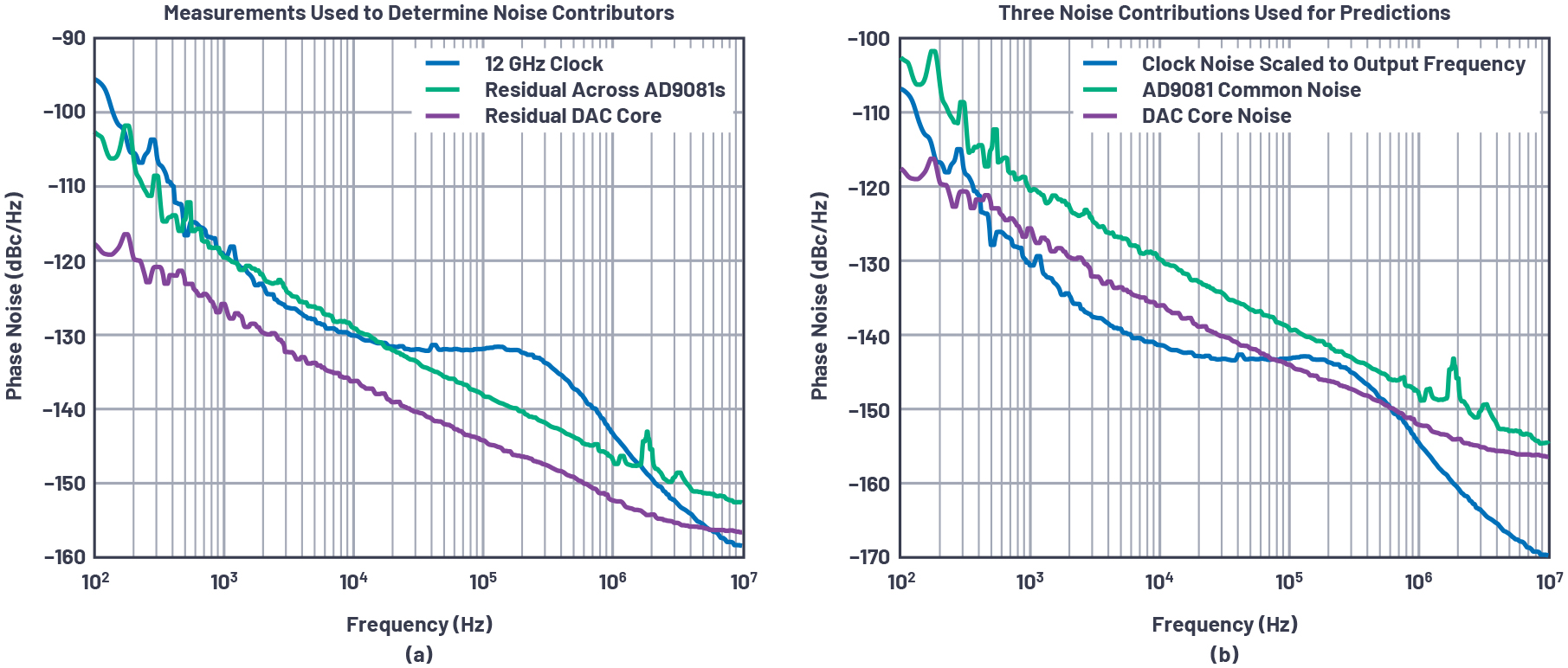
그림 5: (a) 위상 잡음 모델에 사용된 측정 값, (b) 이 모델에서 필요로 하는 위상 잡음 요소 계산. 모든 MxFE들에 하나의 공통 클럭을 사용한 경우이다.

 

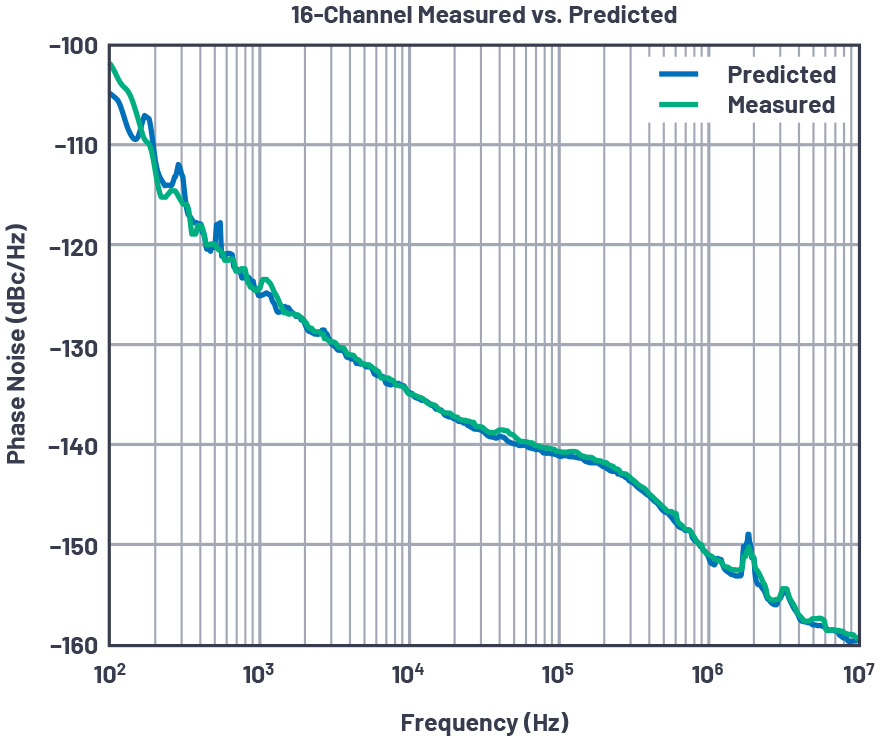
그림 6: 16채널에 대해 3.2GHz로 측정한 결과와 모델 예측

 

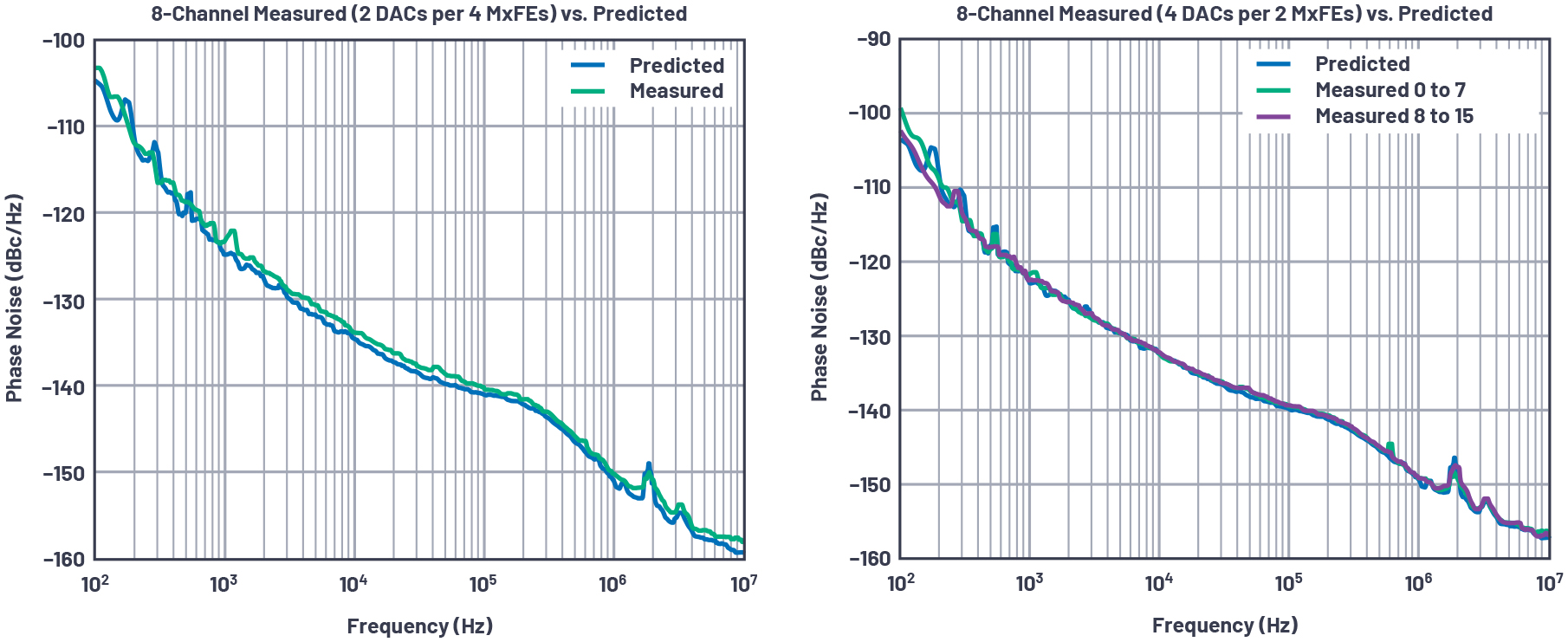
그림 7: 8개 채널에 대해 3.2GHz로 측정한 결과와 모델 예측. 두 플롯에서 차이는 MxFE들에 걸쳐서 송신 채널들을 어떻게 공유하느냐에 따른 것이다.

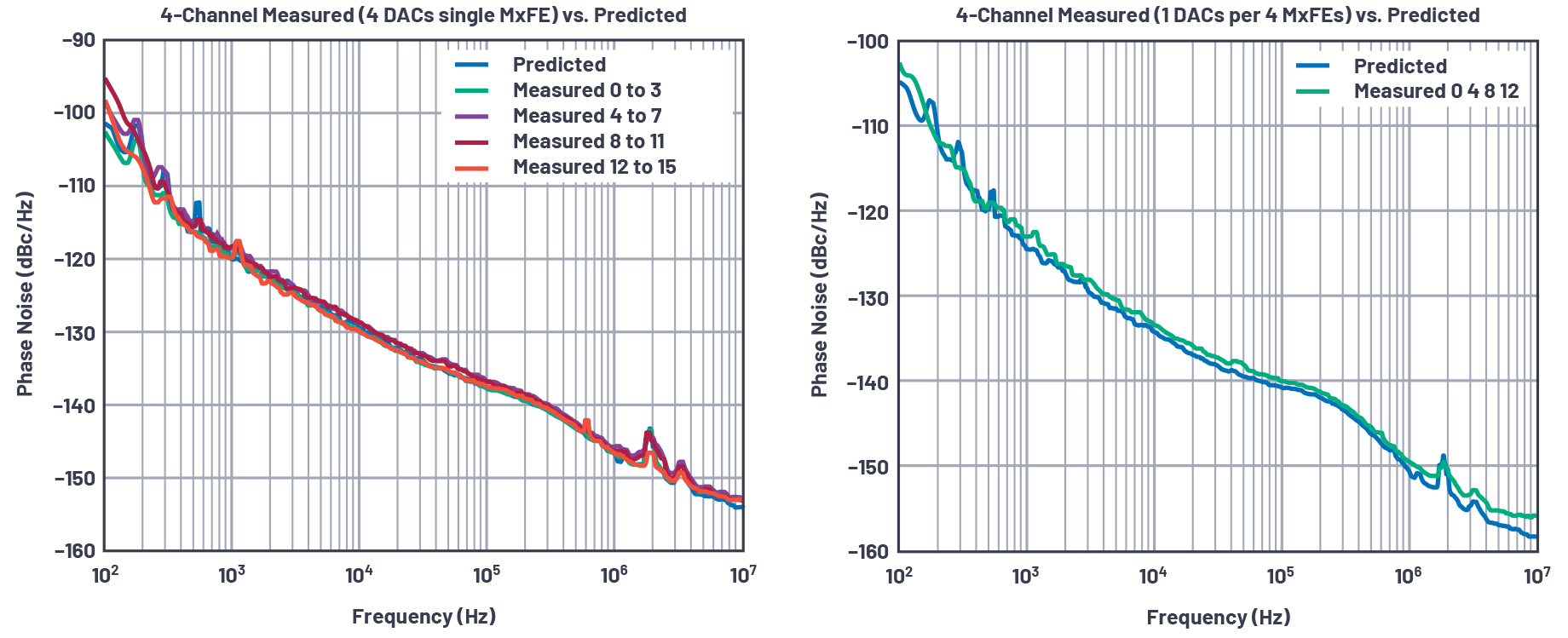
그림 8: 4개 채널에 대해 3.2GHz로 측정한 결과와 모델 예측. 두 플롯에서 차이는 MxFE들에 걸쳐서 송신 채널들을 어떻게 공유하느냐에 따른 것이다.

 

측정 결과와 모델 예측을 비교해 보면 몇 가지 점을 알 수 있다. 대체적으로 모델 예측이 측정 결과와 거의 일치한다. 다만, 몇몇 경우에 측정 결과가 모델 예측보다 약간 낮은 것으로 나타난다. 그림 8의 왼쪽 그래프를 확대해 보면, 모델 예측이 두 측정 사례와는 잘 일치하고, 두 측정 사례는 모델 예측보다 약간 더 높다는 것을 알 수 있다. 이것은 각 MxFE에서 상관 잡음이 AD9081 IC들에 걸쳐서 동일하지 않고 약간씩 차이가 있어서 그러는 것일 수 있다. 또는 몇 가지 전제 하에 공식을 단순화한 것이 이유일 수도 있다. 그렇다 하더라도 이 모델 예측은 상당히 정확하다는 것을 알 수 있다. 이로써 이 특정 설계에 대해 이 접근법이 검증되었다고 본다.

 

측정 사례 2: 각 MxFE에 분산형 PLL 사용

이 측정 사례는 그림 1에서 보듯이 4개의 MxFE 각각에 ADF4371을 별도로 사용했다. ADF4371을 저잡음 500MHz 레퍼런스로 위상 동기화하고 12GHz 출력으로 프로그램했다. 그림 9는 모델에 사용된 측정 값과 모델에 필요로 하는 잡음 요소들을 계산한 것을 보여준다.

 

이 경우에는 PLL이 지배적인 잡음 요소이고 MxFE 잡음은 클럭 잡음보다 훨씬 낮다. 그림 10에서 보듯이, 이 분산형 시스템에 사용된 PLL의 수에 따라서 전반적인 잡음이 향상된다.

 

맺음말

이 글에서는 결합 채널들의 위상 잡음을 꽤 정확하게 예측하는 경험적 모델을 설명했다. 이 접근법의 핵심은, 시스템을 잡음 관점에서 바라보고 블록 다이어그램을 다시 그림으로써 상관적이며 비상관적인 잡음 요소들을 좀더 쉽고 빠르게 파악할 수 있다는 것이다.

 

이 글에서 사용한 “경험적”이라는 용어는 이 제안 기법을 단순히 이론이나 논리가 아니라, 관찰이나 경험으로 검증할 수 있다는 것을 의미한다. 위상 잡음과 관련해서 몇 가지 측정 값을 구하고 이로부터 시스템 전반의 잡음을 체계적으로 계산할 수 있다.

 

이 글에서 사용된 데이터와 공식은 이 특정 하드웨어에서 특수한 것일 수 있다. 하지만 이 접근법은 어떠한 다채널 시스템에나 적용될 수 있다. 그림 11은 좀더 일반적인 블록 다이어그램을 보여준다. 시스템 레퍼런스 오실레이터에서 시작해서 클럭과 LO 분배를 거쳐서 채널 수준 하드웨어에 이르기까지 대규모 시스템에서 잡음 요소들을 체계적으로 파악할 수 있다.

 

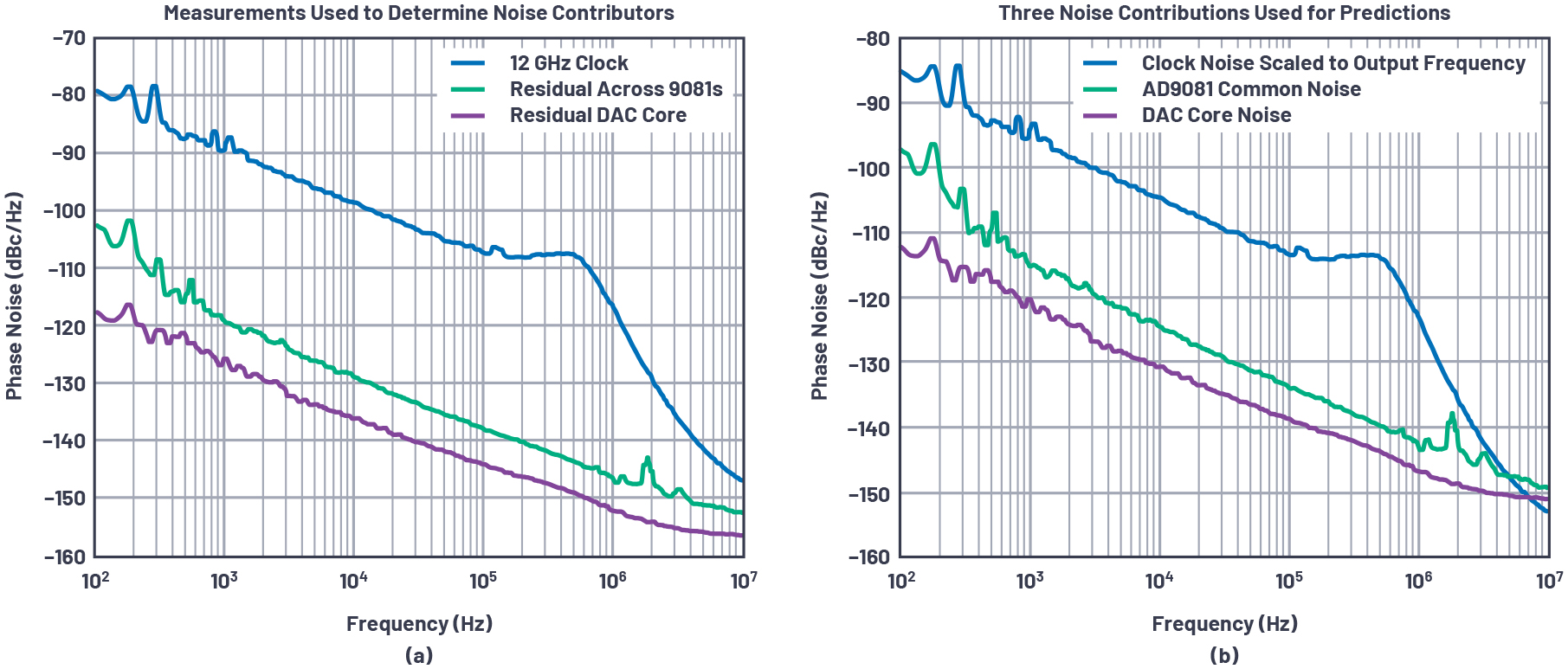
그림 9: (a) 각각 별도의 ADF4371 칩을 클럭 입력 소스로 사용할 때 측정 값. (b) 이 모델에서 필요로 하는 위상 잡음 요소들을 계산한 것. 각 MxFE마다 분산형 PLL을 사용한 경우이다.

 

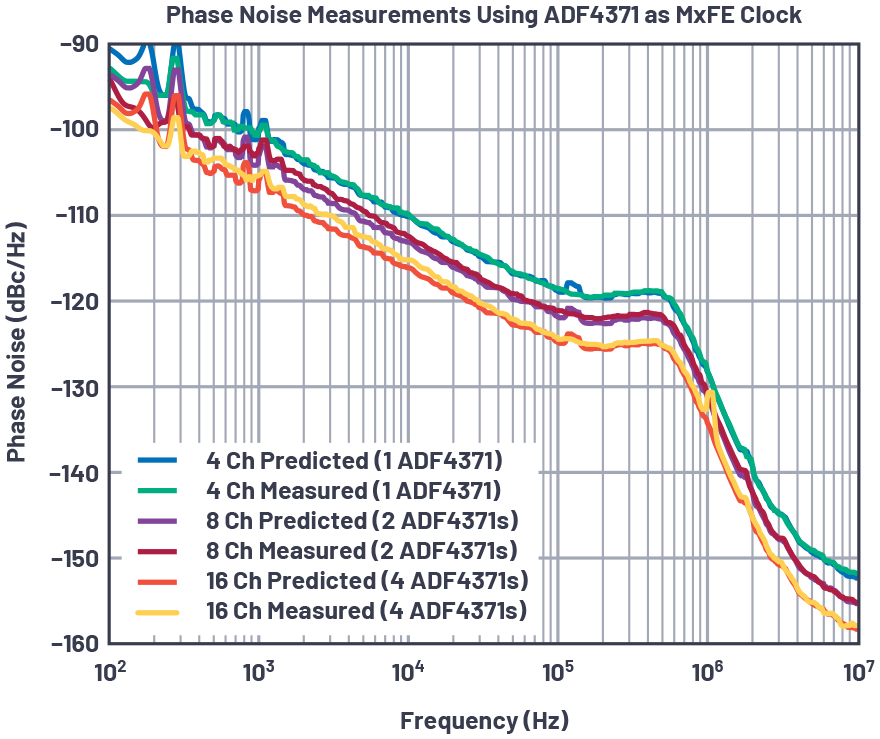
그림 10: ADF4371를 각 MxFE마다 별도의 클럭 소스로서 사용했을 때, 다양한 위상 정렬 송신 채널들을 결합하여 3.2GHz로 측정한 결과와 모델 예측

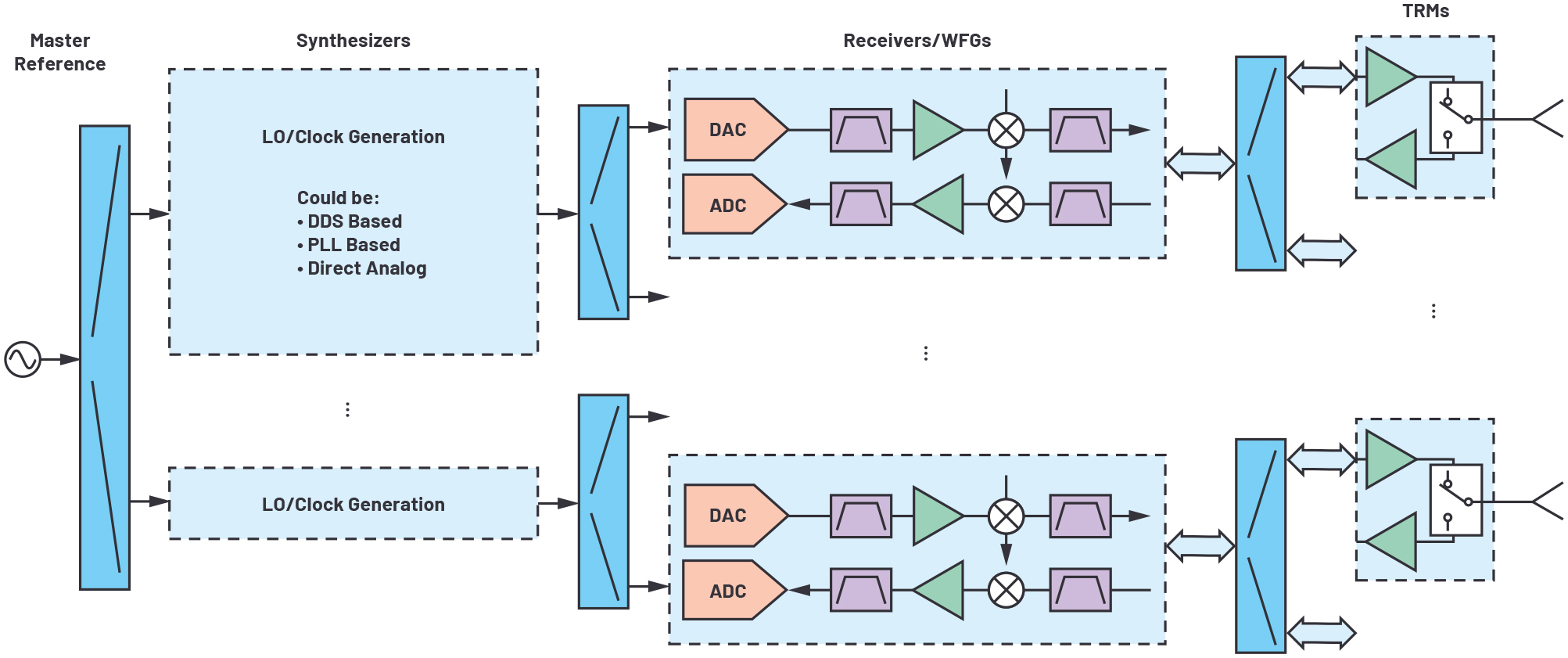
그림 11: 위상 잡음 관점에서 바라본 위상 배열 다이어그램. 모든 신호는 어레이 전반에 걸쳐서 분산된 잡음 성분들을 결합하고 있다. 이 관점에서 시스템 다이어그램을 다시 그림으로써 시스템 차원에서 상관 잡음과 비상관 잡음을 좀더 손쉽게 추적할 수 있다. 시스템 레퍼런스 오실레이터에서 시작해서 클럭 및 LO 분배를 거쳐 채널 수준 하드웨어에 이르기까지 대규모 시스템 전반에 걸쳐서 잡음 요소들을 체계적으로 파악할 수 있다.

 

참고문헌

1 Peter Delos. “System-Level LO Phase Noise Model for Phased Arrays with Distributed Phase-Locked Loops.” Analog Devices, Inc., November 2018.

2 Peter Delos and Mike Jones. “Digital Arrays Using Commercial Transceivers: Noise, Spurious, and Linearity Measurements.” IEEE Phased Array Conference, October 2019.

3 Peter Delos. “Power Supply Modulation Ratio Demystified: How Does PSMR Differ from PSRR?” Analog Devices, Inc., March 2019.

4 Peter Delos and Jarrett Liner. “Improved DAC Phase Noise Measurements Enable Ultralow Phase Noise DDS Applications.” Analog Dialogue, Vo. 51, No. 3, August 2017.

5 Peter Delos. “Phase Locked Loop Noise Transfer Functions.” High Frequency Electronics, January 2016.

6 Peter Delos. “Transceiver Phase Noise Teardown Informs Performance Capability with an External LO.” Analog Devices, Inc., October 2019.

 Jones, Michael, Travis Collins, and Charles Frick. “Integrated Hardened DSP on DAC/ADC ICs Improves Wideband Multichannel Systems.” Analog Devices, Inc., May 2021.

“2-Port Residual Noise Measurements.” Rohde & Schwarz Application Note.

 

저자 소개

피터 딜로스(Peter Delos)는 아나로그디바이스(Analog Devices)의 항공우주 및 방위산업 그룹의 테크니컬 리드이다(노스캐롤라이나주 그린즈버로). 1990년에 버지니아 공대에서 BSEE, 2004년에 NJIT에서 MSEE를 취득했다. 25년 넘게 이 분야에 종사하고 있으며, 경력의 대부분을 아키텍처 레벨, PWB 레벨, 그리고 IC 레벨 첨단 RF/아날로그 시스템 설계에 바쳤다. 현재는 위상 배열 애플리케이션 용으로 고성능 수신기, 파형 생성기, 합성기 설계를 소형화하는 업무를 맡고 있다. 문의: peter.delos@analog.com

 

마이크 존스(Mike Jones)는 아나로그디바이스의 항공우주 및 방위산업 사업부에서 수석 전기 설계 엔지니어이다(노스캐롤라이나주 그린즈버로). 2016년에 아나로그디바이스에 입사했으며, 2007 ~ 2016년까지 제너럴 일렉트릭(GE, 노스캐롤라이나주 윌밍턴)에서 마이크로파 광학 설계 엔지니어로서 원자력용 마이크로파 및 광학 솔루션 개발을 했다. 2004년에 노스캐롤라이나 주립대학에서 BSEE 및 BSCPE, 2006년에 노스캐롤라이나 주립대학에서 MSEE를 취득했다. 문의: mike.jones@analog.com