기술기고문
RF 통신을 위한 디지털 전치왜곡(DPD): 공식부터 구현까지 살펴보기
글: 클레어 마스터슨(Claire Masterson) 시스템 엔지니어 / 아나로그디바이스(Analog Devices, Inc.)
요약
이 글은 디지털 전치왜곡(DPD)의 수학적 기초와 송수신기의 마이크로프로세서 및 하드웨어에서 디지털 전치왜곡을 구현하는 방법에 대해 설명한다. 또한 오늘날의 통신 시스템에서 DPD가 필요한 이유를 살펴보고 수학적 모델이 실제 신호 왜곡을 어떻게 나타내는지 알아본다.
머리말
DPD(digital predistortion)는 많은 RF 엔지니어, 신호 처리 전문가 및 임베디드 소프트웨어 개발자에게 친숙한 약어이다. DPD는 셀룰러 통신 시스템에서 매우 광범위하게 사용되며, 전력 증폭기(PA)가 안테나에 최대 전력을 효율적으로 공급할 수 있게 해준다. 5G 서비스가 본격화되면서 기지국의 안테나 수가 급증하고 스펙트럼이 더욱 혼잡해짐에 따라 DPD는 효율적이고 경제적이면서 규격에 부합하는 셀룰러 시스템을 개발할 수 있는 핵심 기술로 떠오르고 있다.
대부분의 엔지니어들은 순전히 수학적 관점에서든 또는 마이크로프로세서 상에 보다 제한된 구현에서든 저마다의 관점에서 DPD에 대한 나름의 이해를 가지고 있다. 이 글의 목적은 자신의 RF 기지국 설계에서 DPD 성능을 평가하는 엔지니어이거나, 수학적 모델링 기법이 실제 시스템에 어떻게 구현되는지 궁금한 알고리즘 개발자이거나, 누구든 DPD에 대한 지식을 넓히고 보다 완전한 이해를 가질 수 있도록 하는 데 있다.
DPD란 무엇이며, 왜 사용하는가?
RF 신호가 기지국 무선 장치에서 출력되면(그림 1 참조), 신호는 안테나를 통해 전송되기 전에 증폭되어야 한다. 이를 위해 RF PA가 사용된다. 이상적인 세계라면 PA는 입력 신호를 받아서 입력에 비례하는 높은 전력 신호를 출력할 것이다. 또한 증폭기에 제공되는 대부분의 DC 전력 공급이 신호 출력 전원으로 변환되도록 가능한 가장 전력 효율적인 방법으로 이를 수행할 것이다.
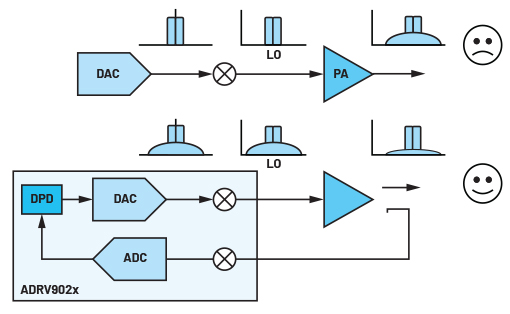
그림 1. DPD를 적용한 무선 구조와, 그렇지 않은 무선 구조의 간략한 블록 다이어그램
그러나, 실제 세계는 이상적인 세계가 아니다. PA는 트랜지스터로 만들어지는데, 트랜지스터는 능동 소자이고 본질적으로 비선형적이다. 그림 2에서 보듯이 PA를 ‘선형’ 영역(여기서 선형은 상대적인 용어이므로 인용 부호로 표시)에서 사용하면 출력 전력은 입력 전력에 비교적 비례한다. 이 방법의 단점은 제공되는 대부분의 전력이 열로 손실되는, 매우 비효율적인 상태에서 PA가 사용되기 쉽다는 것이다. 우리는 종종 포화 지점에서 PA를 사용하기를 원한다. 즉, 이것은 입력 신호를 설정한 양(가령 3dB)만큼 증가시키면, PA 출력이 같은 양만큼 증가하지 않는다는 것을 의미한다(어쩌면 1dB만 증가). 이 지점에서 신호가 증폭기에 의해 상당히 왜곡되는 것은 분명하다.
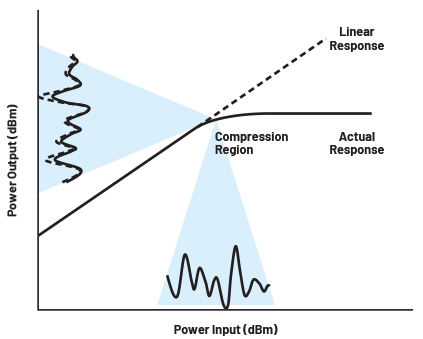
그림 2. PA 입력 전력 대비 출력 전력 곡선(샘플 입/출력 신호를 투사하여 보여준다).
이 왜곡은 입력 신호에 따라 정해진 위치의 주파수 영역에서 발생한다. 그림 3은 이러한 위치가 어디인지, 그리고 기본 주파수와 이들 왜곡 ‘곱(product)’ 간의 관계를 보여준다. RF 시스템에서 보상해야 하는 유일한 왜곡은 기본 신호에 가까운 왜곡이며, 이는 홀수차 상호변조 곱이다. 시스템에서 필터링하는 것은 대역외 곱(고조파 및 짝수차 상호변조 곱)을 처리하는 것이다. 그림 4는 압축 지점 가까이에서 실행되는 RF PA의 출력을 보여준다. 상호변조 곱(특히 3차)을 명확하게 볼 수 있는데, 마치 원하는 신호 주위에 ‘치마’처럼 펼쳐져 보인다.
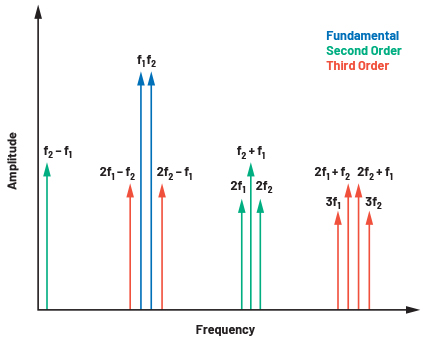
그림 3. 2톤 입력에 대한 상호변조 및 고조파 왜곡 위치
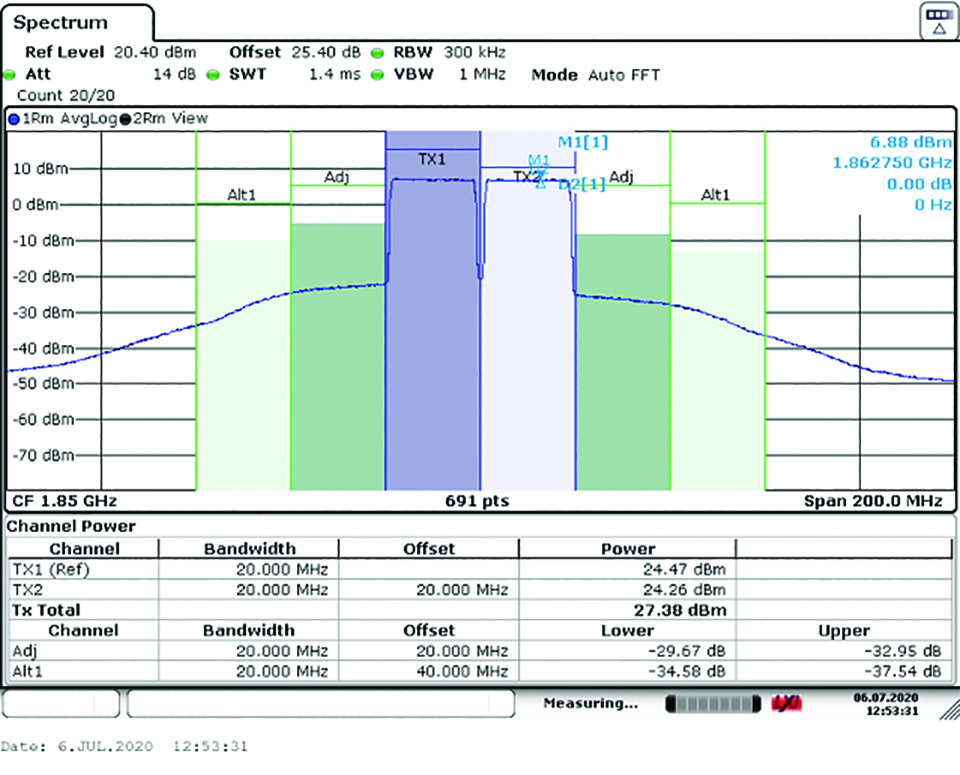
그림 4. SKY66391-12 RF PA를 통과한 2개의 20MHz 반송파. 중심 주파수 = 1850MHz.
DPD는 PA 출력을 관찰하여 원하는 출력 신호가 어떤 것인지 알고 나서, PA 출력이 이상적인 상태에 가깝도록 입력 신호를 변경함으로써 이러한 왜곡을 특성화하는 것을 목표로 한다. 이는 상당히 특정한 환경에서만 효과적으로 수행할 수 있다. 증폭기가 어느 정도 압축되어 비선형 동작 하지만 완전히 포화되지 않도록 증폭기와 입력 신호를 구성해야 한다.
PA 왜곡에 사용되는 기초 수학
그리스 문자나 다른 수학 기호를 보면 과거 대입 시험의 식은땀 나는 순간이 떠오르는 건 비단 필자만의 경험은 아닐 것이다. 사람들은 자신에게 주어진 1차 참고자료 중 하나가 수학으로 가득한 논문이라면 이를 멀리할 수 있다. 논문 ‘RF 전력 증폭기의 디지털 전치왜곡을 위한 일반화된 메모리 다항식 모델‘1은 DPD에 널리 채택되고 있는 일반화된 메모리 다항식(GMP) 접근법을 소개하는 중요한 논문이다. 그러나 신호 처리 측면에 관심이 단순한 취미 수준이라고 한다면 이러한 수학은 다소 무거울 수 있으므로, 먼저 GMP 접근법을 분석하고, 수학으로 무엇을 하는지에 대한 보다 직관적인 이해에 도달하기로 하자.
볼테라 급수(Volterra series)는 DPD의 수학적 뼈대이며, 메모리를 갖는 비선형 시스템을 모델링하는 데 사용된다. 메모리는 간단히 말하면 시스템의 현재 출력이 현재 및 과거 입력에 따라 달라질 수 있음을 의미한다. 볼테라 급수는 매우 일반적이며(따라서 강력함), 전기공학 외에도 많은 분야에서 사용된다. PA DPD의 경우 볼테라 급수를 단순화하여 실시간 디지털 시스템에서 보다 잘 구현할 수 있고 안정적으로 만들 수 있다. GMP는 그러한 간단한 접근법의 하나이다.
그림 5는 GMP를 사용하여 PA의 입력 x와 출력 y 간의 관계를 모델링하는 방법을 보여준다. 수식의 세 개의 개별적인 합산 항목이 서로 매우 유사한 것을 볼 수 있다. 먼저 아래에 빨간색 상자로 표시한 첫 번째 항목에 주목한다. |x(…)|k 항은 입력 신호의 포락선이라고 하며, 여기서 k는 다항식 차수이다. 메모리는 시스템에 통합된다. La = {0,1,2}이면, 모델은 출력 yGMP(n)이 현재 입력 x(n) 및 과거 입력 x(n – 1), 그리고 x(n – 2)에 따라 달라지도록 허용한다.
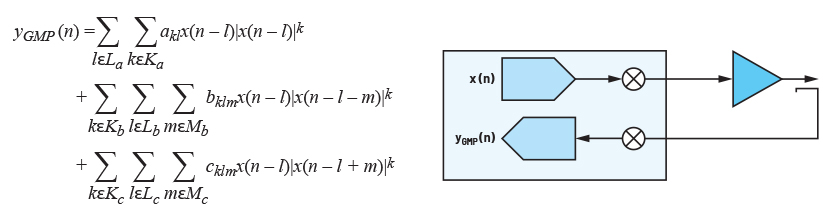
그림 5. PA 왜곡 모델링을 위한 GMP1
그림 6은 샘플 벡터에 대한 다항식 차수 k의 효과를 보여준다. 벡터 x는 단일 20MHz 반송파이며 복소 베이스밴드에 표시된다. GMP 모델링 식은 메모리 성분을 제거하여 단순화한다. x|x|k의 곡선은 그림 4에 보이는 실제 왜곡과 매우 유사하다는 것을 알 수 있다.
각 다항식 차수(k)와 메모리 지연(l)은 관련된 복소 가중치(akl)를 갖는다. 모델의 복잡도를 선택했다면(어떤 k와 l 값을 포함할 것인지), 다음에는 알려진 입력 신호에 대한 PA 출력의 실제 관찰을 기반으로 이러한 가중치를 구해야 한다. 그림 7은 단순화한 식을 행렬 형태로 변환한 것이다. 사용된 수학적 표기는 모델을 간결하게 나타낼 수 있게 한다. 그러나 디지털 데이터의 버퍼에 대한 DPD를 실제 구현하기 위해서는 행렬 표현으로 나타내는 것이 가장 쉽고 보다 잘 대표할 수 있다.
간단한 설명을 위해 그림 6에서 잠시 밀어 놨던 두 번째 및 세 번째 줄의 식을 간단히 살펴보자. m을 0으로 설정하면, 이 두 줄은 첫 번째 줄과 같아진다. 이들 줄은 포락선 항과 복소 베이스밴드 신호 사이에 지연(양의 값과 음의 값 둘 다)을 추가할 수 있게 한다. 이를 지연 및 선행 교차항이라고 하며, DPD의 모델링 정확도를 크게 향상시킬 수 있다. 또한 증폭기의 동작을 모델링하는 시도에 추가적인 자유도를 제공한다. Mb, Mc, Kb, 및 Kc는 0을 포함하지 않는다는 사실에 주의한다. 그렇지 않으면 첫 번째 줄의 항을 반복하게 된다.
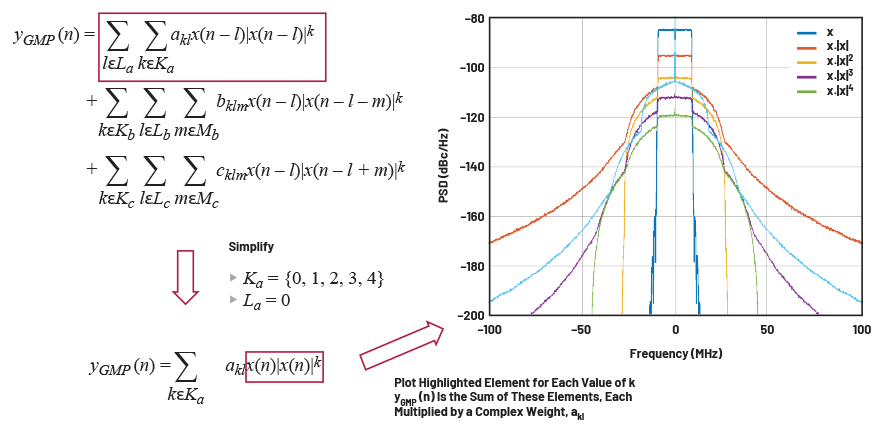
그림 6. 신호 x의 주파수 영역에서 신호에 대한 차수(k)의 효과 그래프
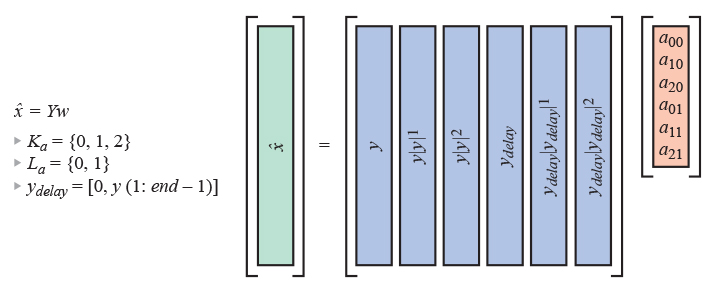
그림 7. 단순화한 식을 데이터 버퍼에 대한 행렬 연산으로 변환한다(디지털로 구현되는 방식에 더 가깝다).
모델의 차수, 메모리 항의 수, 추가해야 하는 교차항은 어떻게 결정할까? 여기에 얼마간의 ‘흑마법’이 필요하다. 왜곡의 물리학에 대한 우리의 지식이 어느 정도 도움이 된다. 증폭기 유형과 제작된 재료, 그리고 이를 통해 재생되는 신호의 대역폭은 모두 모델링 항에 영향을 미치며, 이 분야에 숙련된 엔지니어가 어떤 모델을 사용해야 하는지에 대한 경계를 정할 수 있도록 한다. 하지만 여기에도 어느 정도 시행착오가 수반된다.
이제 모델링 구조를 사용할 수 있으므로, 수학적 관점에서 해결해야 할 문제의 마지막 측면은 가중치 계수의 값을 구하는 것이다. 실제 시나리오에서는 앞에서 설명한 모델의 역함수를 구하는 경향이 있다. 이러한 모델 계수에는 PA 출력이 가능한 선형으로 나타나도록 동일한 가중치를 사용하여 캡처된 PA 출력 벡터를 후치왜곡하여 비선형성을 제거하고 PA를 통해 보내진 전송 신호를 전치왜곡할 수 있다는 점에서 효율적인 상호성이 있음을 보여준다. 그림 8은 가중치 계수 추정과 전치왜곡이 어떻게 수행되는지 나타내는 블록 다이어그램이다.
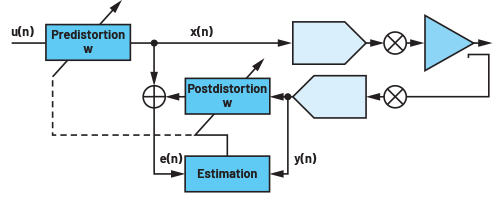
그림 8. 모델링과 전치왜곡의 간접적 구현을 설명하는 블록 다이어그램
역모델의 경우 그림 7에 주어진 행렬 방정식에서 X와 Y의 자리를 바꾸면 X? = Yw가 된다. 여기서 행렬 Y는 그림 9와 같이 다른 경우의 X와 동일한 방식으로 형성된다. 이 예에서는 메모리 항이 포함되었고, 포함된 다항식 차수의 수가 감소되었다. w의 값을 구하려면 Y의 역을 구해야 한다. Y는 정방행렬이 아니므로(길쭉한 직사각형 행렬), ‘의사 역행렬’을 사용하여 수행한다(식 1 참조). 이것은 최소 제곱의 의미에서 w를 구하는 것이므로 즉, X?와 Yw의 차의 제곱을 최소화한다. 바로 우리가 원하는 것이다!

다양한 신호가 있는 실제 환경에서 적용하는 점을 고려하여 이를 좀 더 정교하게 다듬을 수 있다. 여기서 계수는 이전 값에서 업데이트되므로 제한된다. μ는 0과 1 사이의 상수 값으로 반복할 때마다 가중치에 변화를 줄 수 있는 정도를 제어한다. 만약 μ = 1이고 w0 = 0이면, 이 식은 즉시 기본 최소제곱해로 돌아간다. μ를 1보다 작은 값으로 설정하면 계수가 수렴하는 데 여러 번 반복해야 한다.
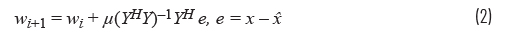
여기에서 설명한 모델링과 추정 기법이 DPD를 수행하는 유일한 방법은 아니다. 동적 편차 감소(DDR) 기반 모델링 같은 기술을 대신 사용하거나 또는 추가로 사용할 수 있다. 계수를 찾기 위해 설명한 추정 기법 역시 다양한 방법으로 수행할 수 있다. 이 글은 책이 아닌 짧은 글이므로 자세한 내용은 책을 참고하길 바란다.
마이크로프로세서에서 어떻게 이를 구현하는가?
수학은 자세히 다루었으므로, 이제는 다음 질문으로 넘어가 실제 통신 시스템에서 이를 어떻게 적용할 것인가를 살펴보자. 이는 일반적으로 마이크로프로세서 또는 FPGA에서 디지털 베이스밴드에 구현된다. ADRV902x 제품군과 같은 ADI의 RadioVerse® 송수신기 제품은 마이크로프로세서 코어를 내장하고 있으며, DPD를 쉽게 구현할 수 있도록 특별히 구성된 구조를 갖추고 있다.
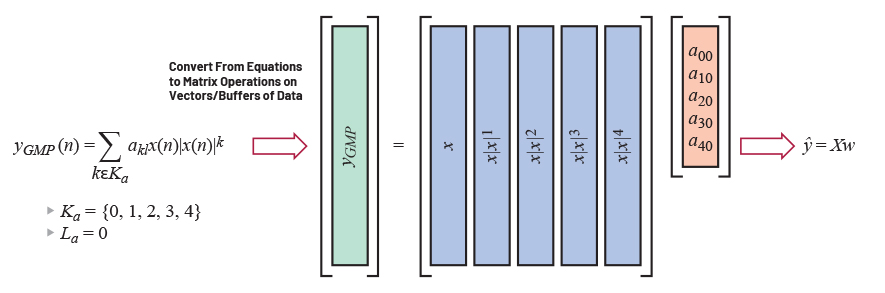
그림 9. 행렬 형태의 역 접근방법 방정식. 여기에는 일부 메모리가 포함되었다.
임베디드 소프트웨어에서 DPD를 구현하는 데에는 두 가지 뚜렷한 측면이 있다. 첫 번째는 실시간 전송되는 데이터의 전치왜곡이 실시간으로 수행되는 DPD 액추에이터이고, 두 번째는 DPD 계수가 PA 출력의 관찰을 바탕으로 업데이트되는 DPD 적응 엔진이다.
DPD와 다른 많은 신호 처리 개념을 마이크로프로세서나 유사한 장치에서 실시간으로 구현하는 방법의 핵심은 룩업 테이블(LUT)을 사용하는 것이다. LUT를 사용하면 비용이 많이 드는 실시간 계산을 간단한 어레이 인덱싱 연산으로 대체할 수 있다. DPD 액추에이터가 전송된 데이터 샘플에 전치왜곡을 어떻게 적용하는지 살펴보자. 표기는 그림 8과 같다. 여기서 u(n)은 전송되는 데이터의 원 샘플이고 x(n)은 전치왜곡된 샘플이다. 그림 10은 주어진 시나리오에서 전치왜곡된 샘플 하나를 얻는 데 필요한 계산을 보여준다. 이 계산은 최고 다항식 차수가 3차이고 단 한 개의 메모리 탭과 단일 교차항만 있는 상대적으로 제한된 예제이다. 이 경우만 해도 하나의 데이터 샘플을 얻는 데 많은 곱셈, 거듭제곱 및 덧셈 계산이 필요하다는 것을 알 수 있다.
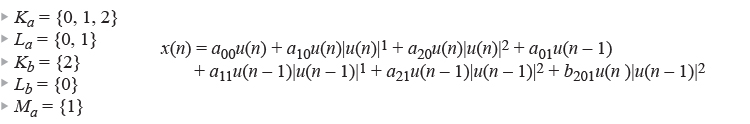
그림 10.한 개의 메모리 탭과 한 개의 3차 교차항이 있는 3차 경우에 대한 전치왜곡 계산
여기에서 실시간 계산의 짐을 덜어주기 위해 LUT가 사용된다. 그림 10은 그림 11처럼 다시 쓸 수 있는데, 그림 11에서는 LUT에 입력되는 데이터가 더 명확해진다. 각 LUT는 |u(n)|에 대해 가능한 많은 수의 값에 대한 식의 진하게 표시된 요소의 결과를 포함한다. 해는 사용 가능한 하드웨어에서 구현할 수 있는 LUT의 크기에 따라 달라진다. 현재 입력 샘플의 크기는 LUT의 해에 따라 양자화되고, 주어진 입력에 대한 올바른 LUT 요소에 액세스하기 위한 인덱스로 사용된다.
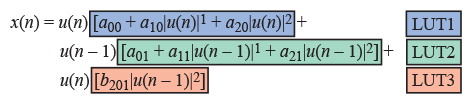
그림 11. 식의 요소를 재그룹화하여 LUT의 구조를 보여준다.
그림 12는 이 예제에서 LUT를 완전한 전치왜곡 액추에이터 구현에 어떻게 통합하는지 보여준다. 이것은 구현 가능한 여러 사례 중 하나일 뿐이다. 동일한 출력을 여전히 유지하면서 변경할 수 있는 한 가지 예는 지연 요소 z–1을 LUT2의 오른쪽으로 이동할 수 있다는 것이다.
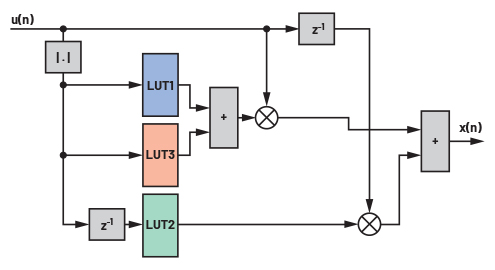
그림 12. LUT를 사용하여 가능한 DPD 구현의 블록 다이어그램
적응 엔진은 액추에이터에서 LUT 값을 계산하는 데 사용되는 계수를 찾는 작업을 수행한다. 여기에는 식 1과 2에 설명된 w 벡터를 구하는 것을 포함한다. 의사 역행렬 연산 (YH Y)-1 YH는 많은 계산을 필요로 한다. 식 1은 다음과 같이 다시 쓸 수 있다.

CYY = YHY이고 CYx = YH x이면 식 3은 다음과 같다.

CYY는 정방행렬이고 숄레스키 분해(Cholesky decomposition)를 사용하여 상부 삼각행렬 L과 켤레전치(CYY =L H L)의 곱으로 분해할 수 있다. 이렇게 하면 더미 변수 z를 도입하고 아래와 같이 풀어 w를 구할 수 있다.

그런 다음 이 더미 변수를 다시 치환하면 다음과 같이 풀 수 있다.

L과 LH는 각각 상부 및 하부 삼각행렬이므로 식 5와 식 6은 w를 찾기 위해 최소의 계산 비용으로 쉽게 풀 수 있다. 적응 엔진을 실행하고 w에 대한 새로운 값이 발견될 때마다 이를 반영하도록 액추에이터 LUT를 업데이트해야 한다. 적응 엔진은 PA 출력의 관찰 또는 전송할 신호의 변화에 대한 운영자의 지식을 바탕으로 설정된 규칙적인 간격 또는 보다 불규칙한 간격으로 수행할 수 있다.
임베디드 시스템에서 DPD를 구현하는 데에는 시스템의 안전성을 보장하기 위해 많은 검사와 밸런싱이 필요하다. 전송된 데이터 버퍼와 캡처 버퍼 데이터가 시간 정렬되어야 한다는 것이 가장 중요한데, 그래야만 이들 사이에 확립된 수학적 관계가 정확하면서 시간이 지남에 따라 적용될 때 참이 유지되도록 보장할 수 있다. 이 정렬이 손실되면, 적응 엔진에서 반환하는 계수가 시스템을 정확하게 전치왜곡하지 못하고, 이에 따라 시스템이 불안정해질 수 있다. 또한 전치왜곡된 액추에이터 출력을 검사하여 신호가 DAC를 포화하지 않도록 보장해야 한다.
결론
지금까지 DPD의 기본 수학과 하드웨어에서의 구현을 살펴보았다. 이 글이 DPD와 관련된 모호함을 해소하는 데 도움이 되었기를 바란다. 이 글은 매력적인 주제에 대한 빙산의 일각일 뿐이며 독자가 통신 시스템에서 신호 처리 기법의 적용을 더 자세히 살펴보는 계기가 되면 좋겠다. 프랫(Pratt)과 커니(Kearney)의 연구는 유선 통신 시스템에서 초광대역폭 사용 사례에 적용되는 DPD에 대한 좋은 자료이다. 2 ADI의 RadioVerse 송수신기 제품은 DPD와 같은 알고리즘을 통합하고 있는 독창적인 제품으로, 고도로 통합된 RF 하드웨어와 구성 가능한 소프트웨어 툴을 고객에게 제공한다.
참고문헌
1 Dennis R. Morgan, Zhengxiang Ma, Jaehyeong Kim, Michael G. Zierdt, and John Pastalan. ‘A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers.’ IEEE Transactions on Signal Processing, Vol. 54, No. 10, October 2006.
2 Patrick Pratt and Frank Kearney. ‘Ultrawideband Digital Predistortion (DPD): The Rewards (Power and Performance) and Challenges of Implementation in Cable Distribution Systems.’ Analog Dialogue, Vol. 51, No. 3, July 2017.
###
저자 소개
클레어 마스터슨(Claire Masterson)은 아나로그디바이스(리머릭) 무선 시스템 그룹의 시스템 엔지니어로서 시스템 구현, 소프트웨어 개발, 알고리즘 개발 및 검증을 담당하고 있다. 트리니티 칼리지 더블린에서 공학 학사 및 박사 학위를 받았으며, 졸업 후 2011년에 ADI에 입사했다. 실제 시스템, 특히 5G 및 6G 시스템 개발과 차세대 DPD 구현에서 디지털 신호 처리의 적용에 관심을 가지고 있다. 문의: claire.masterson@analog.com.

제품스펙